| Вестник ОмГУ | Выпуск | Тематика | Литература |
| Вестник Омского университета, 1999,
Вып. 4. С. 32-33. © Омский государственный университет, 1999 |
УДК 539.12:530.145 |
В.В. Клишевич
Омский государственный университет,
кафедра теоретической физики
644077, Омск, пр. Мира, 55-А
Получена 14 апреля 1999 г.
| We have integrated the Dirac equation in Riemannian space with four dimentional motion group. This Riemannian space is stackel, but Dirac equation not admit the separation of variables. |
Статья является продолжением предыдущей статьи. Рассмотрим риманово пространство с линейным элементом (формула (32.8) в монографии А.З. Петрова [1, c.285]):
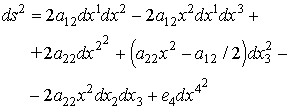 |
(1) |
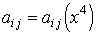 - произвольные функции,
- произвольные функции,
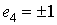 ,
, 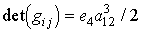 .
.
Пространство (1) допускает четыре вектора Киллинга (см.там же [1]), они принимают следующие значения:
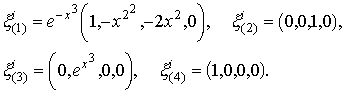 |
Для построения оператора Дирака и его операторов симметрии
применим метод тетрад. Положим 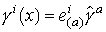 , где
, где
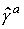 - постоянные матрицы Дирака (со шляпками) в
стандартном представлении,
- постоянные матрицы Дирака (со шляпками) в
стандартном представлении, 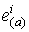 - ортогональная тетрада, которая
расщепляет постоянную метрику
- ортогональная тетрада, которая
расщепляет постоянную метрику 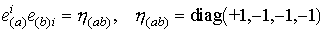 - матрица Минковского.
- матрица Минковского.
Ортогональную тетраду для метрики (1) реализуем в виде:
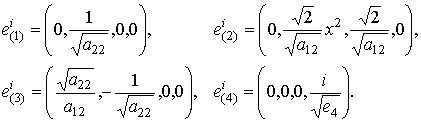 |
Оператор Дирака в пространстве (1) имеет вид:
 |
(2) |
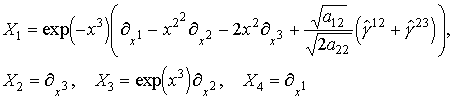 |
образуют алгебру Ли, обозначим ее символом 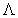 со следующими
коммутационными соотношениями:
со следующими
коммутационными соотношениями:
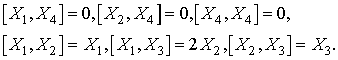 |
Алгебра 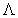 изоморфна алгебре операторов симметрии первого
порядка уравнения Клейна-Фока
изоморфна алгебре операторов симметрии первого
порядка уравнения Клейна-Фока 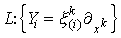 .
Используя необходимые условия существования спинорных полей, полученные
в статье [2], можно показать, что пространство (1)
в общем случае не допускает ни тензорного поля Яно-Киллинга, ни векторного
поля Яно. В самой алгебре
.
Используя необходимые условия существования спинорных полей, полученные
в статье [2], можно показать, что пространство (1)
в общем случае не допускает ни тензорного поля Яно-Киллинга, ни векторного
поля Яно. В самой алгебре 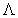 отсутствует тройка коммутирующих операторов
первого порядка, и провести стандартную процедуру разделения переменных,
рассмотренную в [2], не представляется возможным. Само пространство
(1) является штеккелевым, тип (2.1).
отсутствует тройка коммутирующих операторов
первого порядка, и провести стандартную процедуру разделения переменных,
рассмотренную в [2], не представляется возможным. Само пространство
(1) является штеккелевым, тип (2.1).
Мы проведем некоммутативное интегрирование уравнения Дирака в пространстве (1).
Легко проверить, что для алгебры симметрии L выполнено условие
dimL + indL = 6
теоремы о некоммутативной интегрируемости [3]. Выбор
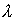 -представления
алгебры симметрии L позволяет найти базис решений уравнения Дирака
-представления
алгебры симметрии L позволяет найти базис решений уравнения Дирака
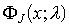 из решения системы дифференциальных уравнений:
из решения системы дифференциальных уравнений:
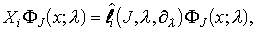 |
(3) |
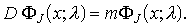 |
(4) |
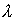 - представление алгебры симметрии зададим
дифференциальными операторами:
- представление алгебры симметрии зададим
дифференциальными операторами:
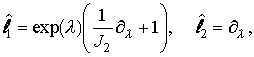 |
(5) |
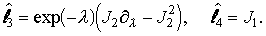 |
(6) |
Операторы Казимира для алгебры симметрии 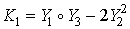 ,
,
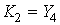 (символ - о означает симметризацию -
(символ - о означает симметризацию -
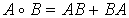 в
в 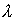 - представлении
имеют вид:
- представлении
имеют вид: 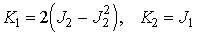 .
Общее решение системы (5) находится методом характеристик:
.
Общее решение системы (5) находится методом характеристик:
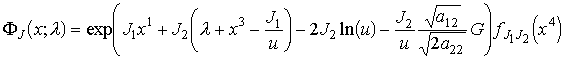 |
(7) |
здесь  , матрица
, матрица 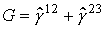 ,
спинор
,
спинор 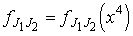 зависит только от одной переменной
x4 и параметров J1 и J2.
Подставим общее решение (3) в уравнение (6) и
домножим это уравнение слева на фактор
зависит только от одной переменной
x4 и параметров J1 и J2.
Подставим общее решение (3) в уравнение (6) и
домножим это уравнение слева на фактор 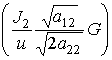 .
Используя формулы разложения для
.
Используя формулы разложения для 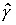 -матриц:
-матриц:
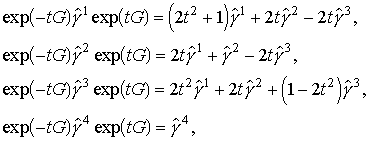 |
где нужно положить 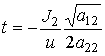 ,
получим обыкновенное дифференциальное уравнение на неизвестный спинор:
,
получим обыкновенное дифференциальное уравнение на неизвестный спинор:
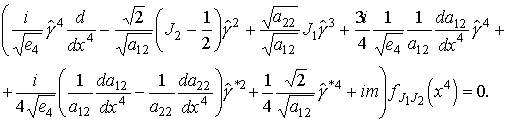 |
Решив это уравнение, мы получим решение уравнения Дирака в римановом пространстве (1) в виде (3).
Формула (3) определяет движение свободной частицы со спином 1/2 в искривленном пространстве (1).
Результаты статьи можно использовать для нахождения точных решений
уравнения Дирака в пространстве (1).
| [1] | Петров А.З. Пространства Эйнштейна. М.: Наука, 1961. |
| [2] | Клишевич В.В. // Известия вузов. Физика. 1999. N6. C.1-5. |
| [3] | Шаповалов А.В., Широков И.В. // ТМФ. 1995. Т.104. \No 2. C.195--213. |
| [4] | Шаповалов В.Н. // Известия вузов. Физика. 1975. \No 6. C.57-63. |