![]()
(1)
| Вестник ОмГУ | Выпуск | Тематика | Литература |
| Вестник Омского университета, 1999,
Вып. 3. С. 53-55. © Омский государственный университет, 1999 |
УДК: 539.12:530.145 |
В.В. Клишевич
Омский государственный университет,
кафедра теоретической физики
644077, Омск, пр. Мира, 55-А
Получена 14 апреля 1999 г.
| We have integrated the Dirac and Klein-Fok equations in Riemannian space with four dimentional motion group. This Riemannian space is stackel, but Dirac equation not admit the separation of variables. We have also found in this space Einstein equation exact solution. |
1. Предварительные сведения и постановка задачи
Предлагаемая статья является непосредственным продолжением статьи [1], посвященной методам интегрирования уравнения Дирака в римановом пространстве с четырехмерной группой движений. Пространства с группами движений являются наиболее привлекательными для различных физических приложений. Эти пространства богаты симметриями, и в то же время компонентами метрического тензора могут служить произвольные функции, что дает значительную свободу действий при изучении релятивистских волновых уравнений. Данная статья посвящена вопросам интегрирования одного из основных уравнений релятивистской физики - уравнения Дирака. Дадим основные определения, следуя в основном обозначениям статей [1]; [2]. Уравнение Дирака в четырехмерном римановом пространстве запишем в виде:
|
(1) |
Здесь Pk=i(Сk+Gk), Сk
- оператор ковариантной производной; Gk
- спинорная связность, на которую наложено
условие [Pk,gk]
= 0, Sp(Gi) = 0. Как показано в
работе [3], для спинорной связности можно
использовать явную формулу: Gi
= -1/4gk;igk.
Матрицы Дирака в римановых пространcтвах
определяются как произвольное, но фиксированное
решение уравнения ![]() , где
, где ![]() - единичная матрица; g ij -
метрический тензор; m - const. Общий вид
операторов симметрии для уравнения (1) указан,
например, в работе В.Н. Шаповалова [2]:
- единичная матрица; g ij -
метрический тензор; m - const. Общий вид
операторов симметрии для уравнения (1) указан,
например, в работе В.Н. Шаповалова [2]:
|
(2) |
|
(3) |
|
(4) |
Здесь
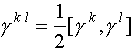 ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() - полностью
антисимметричный тензор (e1234
= 1). Символ ;k означает ковариантную
производную по координате xk
относительно метрики, по повторяющимся индексам
подразумевается суммирование.
- полностью
антисимметричный тензор (e1234
= 1). Символ ;k означает ковариантную
производную по координате xk
относительно метрики, по повторяющимся индексам
подразумевается суммирование.
Векторное поле x k в
формуле (2) определяется из уравнения xi;k + xk;i
= 0 и называется векторным полем Киллинга.
Тензорное поле в формуле (3) находится из
уравнений: fij + fji = 0, fij;k
= eijkl gl, где gl -
некоторый вектор, и называется тензорным полем
Яно-Киллинга. На векторное поле в уравнении (4)
имеется формула fi; j = 1/4gij f k;k,
fi = h ;i, fi
= h ;i, здесь h - скаляр, это векторное поле
называется полем Яно. Уравнения на эти поля
получены в [2]. Для построения операторов
(1) - (4) применим метод тетрад. Положим ![]() , где
, где ![]() - постоянные матрицы Дирака (со
шляпками) в стандартном представлении,
- постоянные матрицы Дирака (со
шляпками) в стандартном представлении, ![]() - ортогональная
тетрада, которая расщепляет постоянную метрику
- ортогональная
тетрада, которая расщепляет постоянную метрику ![]() ,
, ![]() - матрица Минковского. Линейный
элемент рассматриваемого риманова пространства
имеет вид (формула (32.4) в монографии А.З. Петрова [4,стр.284]):
- матрица Минковского. Линейный
элемент рассматриваемого риманова пространства
имеет вид (формула (32.4) в монографии А.З. Петрова [4,стр.284]):
|
(5) |
здесь aij = aij (x4) - произвольные функции, e4 = ±1, det(gij) = a211a22e4. Пространство (5) допускает четыре вектора Киллинга (см. там же [4]), они имеют следующий вид: x i(1) = (0,1,0,0), x i(2) = (0,0,1,0), x i(3) = (-1,x3,0,0), x i(4) = (-x3, (x32-x12)/2, x1,0). Ортогональную тетраду для метрики (5) реализуем в виде:
|
Оператор Дирака (1) в пространстве (5) имеет вид:
|
Киллинговы операторы симметрии (2) для уравнения Дирака:
|
образуют алгебру Ли со следующими
коммутационными соотношениями:
[X1,X2] = 0, [X1,X3]
= 0, [X1,X4] = 0, [X2,X3]
= X1, [X2,X4] = X3,
[X4,X3] = X2.
В дальнейшем эту алгебру будем обозначать
символом L. Алгебра L является разрешимой и не
содержит тройки коммутирующих операторов
первого порядка. Отметим, что она изоморфна
алгебре симметрии L уравнения Клейна-Фока ![]() . Наша цель
состоит в том, чтобы проинтегрировать уравнение
Дирака (1) в римановом пространстве (5).
. Наша цель
состоит в том, чтобы проинтегрировать уравнение
Дирака (1) в римановом пространстве (5).
2. Интегрирование уравнения Дирака
Используя необходимые условия спинорных полей, полученные в [5], можно показать, что в общем случае пространство (5) не допускает ни тензорного поля Яно-Киллинга, ни векторного поля Яно. В самой алгебре симметрии L отсутствует тройка коммутирующих операторов, и провести процедуру разделения переменных в рамках стандартного определения, которое рассмотрено в [1], не представляется возможным. Тем не менее выполнено условие dim L + ind L = 6 теоремы о некоммутативной интегрируемости [6]. Выбор l-представления алгебры L позволяет найти базис решений уравнения (1) FJ(x;l) из решения системы дифференциальных уравнений:
|
(6) |
|
(7) |
l-представление алгебры Ли L реализуем дифференциальными операторами:
|
(8) |
Операторы Казимира для алгебры L: K1=Y1, K2=Y22 + Y32 - 2Y1 Y4 в l-представлении имеют вид: K1= J1, K2=J1(i-2J2). Общее решение системы (6) находится методом характеристик:
|
(9) |
здесь u = x3-il, u =x1 - iu, спинор fJ1J2
= fJ1J2(x4)
зависит только от одной переменной x4 и
параметров J1 и J2. Подставим
общее решение (9) в уравнение (7) и домножим это
уравнение слева на фактор ![]() . Используя формулы разложения
для
. Используя формулы разложения
для ![]() -матриц
-матриц
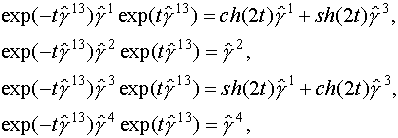
где нужно положить t = ln(u)
/ 2, получим обыкновенное дифференциальное
уравнение на неизвестный спинор:
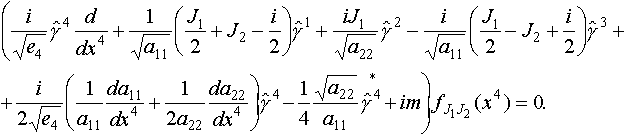
Решив это уравнение, мы получим решение
уравнения Дирака в виде (9).
3. Интегрирование уравнения Клейна-Фока
Уравнение Клейна-Фока в римановом пространстве (5)
|
(10) |
в отличие от уравнения Дирака, можно решить методом разделения переменных без каких-либо ограничений на метрику. Пространство (5) является штеккелевым, тип (2.1). В качестве полного коммутативного набора укажем тройку операторов {Y1;Y2;Y22 + Y32-2Y1Y4}. Решение уравнения (10) в пространстве (5) представимо в разделенных переменных
|
(11) |
здесь Hs(z) - функция Эрмита,
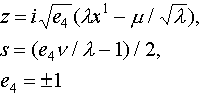 ,
,
функция удовлетворяет уравнению
|
(12) |
l,m,n- существенные параметры разделения.
Для полноты изложения приведем решение уравнения (10) методом некоммутативного интегрирования. Мы используем l-представление алгебры L, задаваемое операторами (8). Решение системы (6) имеет вид:
|
(13) |
здесь u = x3-il, v = x1 - i u. Подставляя это решение в формулу (10), получим обыкновенное дифференциальное уравнение
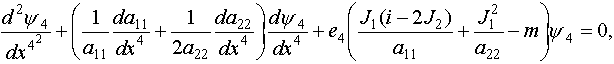
которое совпадает, при подходящем определении параметров, с уравнением (12).
В заключение отметим, что метрика (5) удовлетворяет вакуумным уравнениям Эйнштейна
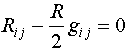
здесь Rij - тензор Риччи; R - скалярная кривизна, если функции, входящие в метрику, принимают значения a11=c x42/3, a22=4 c2 x4-2/3/(9e4), c - const (при поиске решений для функций aij предполагался степенной вид, общая ситуация не рассмотрена). Таким образом, данный случай дает нам пример штеккелева пространства, в котором выполняются уравнения Эйнштейна, однако свободное уравнение Дирака не интегрируется стандартным способом разделения переменных.
4. Заключение
Решение уравнения Дирака (9) определяет движение свободной частицы со спином 1/2 в искривленном пространстве (5). Аналогично формулы (11) или (13) определяют движение скалярной частицы в том же пространстве. Результаты статьи можно использовать для нахождения точных решений уравнения Дирака и Клейна-Фока в пространстве (5).
| [1] | Клишевич В.В. // Известия вузов. Физика. 1999. 6. C.11-17. |
| [2] | Шаповалов В.Н. // Известия вузов. Физика. 1975. 6. C.57-63. |
| [3] | Клишевич В.В. // Вестник Омского университета. Физика. 1999. 4. C.19-21. |
| [4] | Петров А.З. Пространства Эйнштейна. М.: Наука, 1961. |
| [5] | Клишевич В.В. // Известия вузов. Физика. 1999. 7. C.24-29. |
| [6] | Шаповалов А.В., Широков И.В. // ТМФ. 1995. Т.104. 2. C.195-213. |