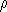 -mixing
triangular arrays of random variables are obtained. These conditions
generalize known results of such type.
-mixing
triangular arrays of random variables are obtained. These conditions
generalize known results of such type.| Вестник ОмГУ | Выпуск | Тематика | Литература |
| Вестник Омского университета, 1999, Вып. 2. С. 14-16. © Омский государственный университет, 1999 |
УДК 519.214.5 |
А.Г. Гринь
Омский государственный университет, кафедра математического анализа
644077 Омск, пр. Мира, 55-A
Получена
The sufficient conditions for central limit theorem for 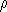 -mixing
triangular arrays of random variables are obtained. These conditions
generalize known results of such type. -mixing
triangular arrays of random variables are obtained. These conditions
generalize known results of such type. |
Пусть 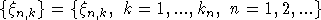 -
последовательность серий случайных величин, заданных на одном
вероятностном пространстве,
-
последовательность серий случайных величин, заданных на одном
вероятностном пространстве, 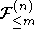 ,
,
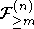 -
-  -алгебры,
порожденные семействами
-алгебры,
порожденные семействами 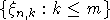 и
и
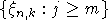 .
.
Говорят, что 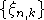 удовлетворяет условию полной регулярности
(
удовлетворяет условию полной регулярности
(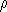 -перемешивания), если
-перемешивания), если
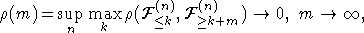
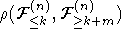 - максимальный коэффициент корреляции между
- максимальный коэффициент корреляции между
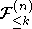 и
и 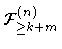 .
.
(Здесь и далее если в максимумах, суммах и т.п. не указаны пределы изменения переменной k, то предполагается, что k меняется от 1 до kn.)
Будем писать 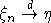 в случае, когда
в случае, когда 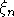 сходятся к
сходятся к 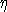 по распределению, а
по распределению, а 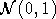 будет обозначать случайную
величину, имеющую нормальное распределение с параметрами 0 и 1.
Пусть
будет обозначать случайную
величину, имеющую нормальное распределение с параметрами 0 и 1.
Пусть 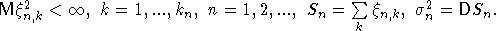 Если
Если
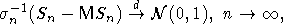
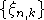 применима центральная предельная теорема.
применима центральная предельная теорема.
Последовательность случайных величин 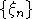 будет интерпретироваться
как последовательность серий, у которой
будет интерпретироваться
как последовательность серий, у которой 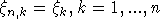 .
.
В дальнейшем будут использоваться также следующие понятия и обозначения.
Если функции f и g связаны соотношением 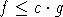 ,
где с>0 не зависит от аргументов функций f и g, то будем писать
,
где с>0 не зависит от аргументов функций f и g, то будем писать
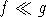 .
Через 1(A) будем обозначать индикатор множества A.
.
Через 1(A) будем обозначать индикатор множества A.
Для стационарных последовательностей И.А. Ибрагимов в [1] и [2] получил следующие результаты.
Теорема 1.
Пусть 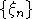 - стационарная последовательность, удовлетворяющая
условию
- стационарная последовательность, удовлетворяющая
условию 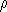 -перемешивания,
-перемешивания, 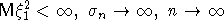 и пусть выполнено одно из следующих
предположений:
и пусть выполнено одно из следующих
предположений:
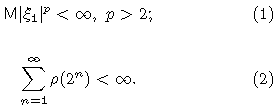
Тогда к последовательности 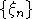 применима центральная предельная
теорема.
применима центральная предельная
теорема.
Замечение 1.
Об условиях в результатах И.А. Ибрагимова. Условие
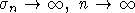 исключает единственную вырожденную
ситуацию, описанную в [1]; эту стуацию также можно исключить,
предположив, например, что
исключает единственную вырожденную
ситуацию, описанную в [1]; эту стуацию также можно исключить,
предположив, например, что 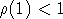 (см.[3]).
(см.[3]).
Условия (1) и (2) являются неулучшаемыми в следующем смысле. Р.Бредли в
[4] показал, что существуют стационарные последовательности,
удовлетворяющие условию 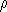 -перемешивания, у которых
-перемешивания, у которых 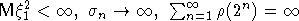 и для которых не выполняется центральная предельная теорема.
и для которых не выполняется центральная предельная теорема.
Сказанное в замечании 1 можно сформулировать еще так: условие (2) является
"минимальным" предположением о скорости стремления коэффициента 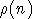 к нулю, при котором центральная предельная теорема справедлива при тех же
предположениях о распределениях
к нулю, при котором центральная предельная теорема справедлива при тех же
предположениях о распределениях 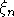 ,
что и для последовательностей
независимых случайных величин. А.Г. Гринь в [5] показал, что это
утверждение остается справедливым и для схем серий. Однако, как показывает
первый из названных результатов И.А. Ибрагимова, для последовательностей с
,
что и для последовательностей
независимых случайных величин. А.Г. Гринь в [5] показал, что это
утверждение остается справедливым и для схем серий. Однако, как показывает
первый из названных результатов И.А. Ибрагимова, для последовательностей с
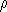 -перемешиванием центральная предельная теорема может выполняться
и при нарушении предположения (2), но, естественно, при дополнительных
условиях на распределения
-перемешиванием центральная предельная теорема может выполняться
и при нарушении предположения (2), но, естественно, при дополнительных
условиях на распределения 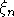 .
Условия такого типа были получены
М.Пелиград в [6]; приведем здесь ее результат в виде теоремы.
.
Условия такого типа были получены
М.Пелиград в [6]; приведем здесь ее результат в виде теоремы.
Теорема 2. Пусть 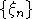 - стационарная последовательность,
удовлетворяющая условию
- стационарная последовательность,
удовлетворяющая условию 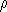 -перемешивания,
-перемешивания, 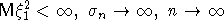 и пусть
и пусть
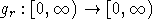 - неубывающая функция, удовлетворяющая условию
- неубывающая функция, удовлетворяющая условию
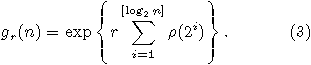
Тогда если
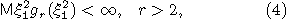
то к последовательности 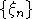 применима центральная предельная
теорема.
применима центральная предельная
теорема.
Замечание 2.
Условие (4) в теореме 1 является неулучшаемым в следующем смысле. Р.Бредли в [4] показал,что существует r>0 такое, что если функция h(x) удовлетворяет условию
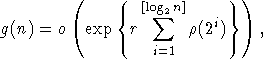
то (при некоторых технических предположениях) можно построить стационарную
последовательность 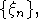 удовлетворяющую условию
удовлетворяющую условию 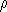 -
перемешивания, у которой
-
перемешивания, у которой 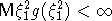 и к которой не применима центральная предельная теорема.
и к которой не применима центральная предельная теорема.
В настоящей заметке приведенные выше результаты обобщаются на схемы серий.
Если последовательность серий 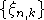 удовлетворяет условию
удовлетворяет условию
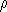 -перемешивания с
-перемешивания с 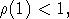 то
то
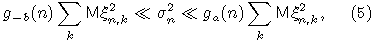
где gr(n) определяется соотношением (3), а 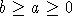 .
Правое неравенство доказано в [7] с a=6,
а левое - в [3] с b=16. В принципе эти оценки можно
уточнять, например, для стационарных последовательностей в [6]
неравенства (5) доказаны с любыми a и b такими,что 1<a<b. Перенеся
приемы, используемые в [6], на схемы серий, можно получить неравенства
(5) с любыми
.
Правое неравенство доказано в [7] с a=6,
а левое - в [3] с b=16. В принципе эти оценки можно
уточнять, например, для стационарных последовательностей в [6]
неравенства (5) доказаны с любыми a и b такими,что 1<a<b. Перенеся
приемы, используемые в [6], на схемы серий, можно получить неравенства
(5) с любыми 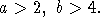
Обозначим
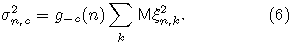
Введем стандартное для предельных теорем в схеме серий условие равномерной предельной малости слагаемых:
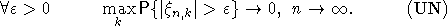
Следующая теорема является основным результатом настоящей работы.
Теорема 3.
Пусть 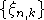 -последовательность серий случайных величин,
удовлетворяющая условию (UN) и условию
-последовательность серий случайных величин,
удовлетворяющая условию (UN) и условию 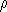 -перемешивания с
-перемешивания с 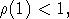 и, следовательно, справедливы оценки (5).
Пусть далее
и, следовательно, справедливы оценки (5).
Пусть далее 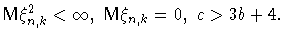 Тогда если
Тогда если
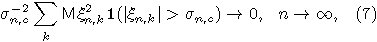
где 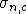 определяется соотношением (6),то к последовательности
серий
определяется соотношением (6),то к последовательности
серий 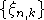 применима центральная предельная теорема.
применима центральная предельная теорема.
Замечание 3. Ясно, что условие (7) является аналогом известного условия Линдеберга. Нетрудно вывести, что теорема 2 останется справедливой, если условие (7) заменить на следующее условие "в форме Ляпунова":
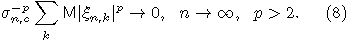
Замечание 4. Из элементарных свойств медленно меняющихся функций (см.,
например, [1]) следует, что при любом 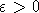 и любом
и любом
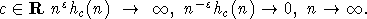 Если же выполнено условие (2), то
Если же выполнено условие (2), то
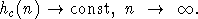 С учетом этого из теоремы 3 легко выводятся результаты
И.А. Ибрагимова в теореме 1.
С учетом этого из теоремы 3 легко выводятся результаты
И.А. Ибрагимова в теореме 1.
Схема доказательства теоремы 3.
Пусть 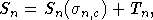 где
где
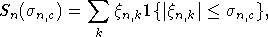
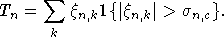
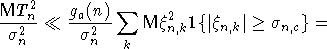
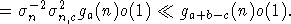
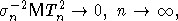
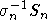 и
и 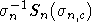 совпадают и
совпадают и
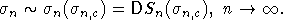
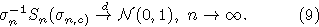
Для того чтобы выполнялось (9), достаточно, чтобы последовательность
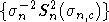 была равномерно интегрируемой.
Для стационарных последовательностей, удовлетворяющих различным
условиям перемешивания, этот факт неоднократно передоказывался
многими авторами (см.,например, [8]). На схемы серий этот результат
переносится без особых сложностей. В свою очередь, равномерная
интегрируемость последовательности
была равномерно интегрируемой.
Для стационарных последовательностей, удовлетворяющих различным
условиям перемешивания, этот факт неоднократно передоказывался
многими авторами (см.,например, [8]). На схемы серий этот результат
переносится без особых сложностей. В свою очередь, равномерная
интегрируемость последовательности 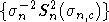 будет иметь место, если будет доказано, что при некотором
будет иметь место, если будет доказано, что при некотором 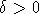
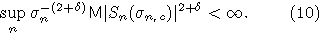
Будем доказывать (10) при 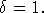 Обозначим
Обозначим
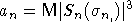 .
Комбинируя приемы,используемые в
[1] и [7] при доказательстве оценок для an и
.
Комбинируя приемы,используемые в
[1] и [7] при доказательстве оценок для an и 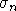 ,
можно получить соотношение
,
можно получить соотношение
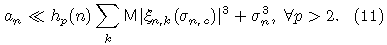
Используя соотношения (7) и (8), выводим
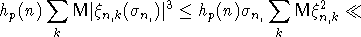
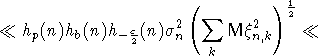
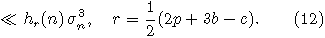
Так как c>3b+4, то константу p>2 в соотношении (11) можно подобрать
такой, чтобы 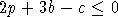 .
Тогда из (11) и (12) вытекает, что
.
Тогда из (11) и (12) вытекает, что
 т. е. имеет место (10),
а вместе с ним - (9). В силу сказанного выше это означает, что теорема 3
доказана.
т. е. имеет место (10),
а вместе с ним - (9). В силу сказанного выше это означает, что теорема 3
доказана.
(1) Работа выполнена при поддержке Российского фонда фундаментальных исследований, грант 99-01-01130 и программы интеграции науки и высшей школы, грант 586.
| [1] | Ибрагимов И.А., Линник Ю.В. Независимые и стационарно связанные величины. М.: Наука, 1965. 524 с. |
| [2] | Ибрагимов И.А. Замечание о центральной предельной теореме для зависимых случайных величин// Теория вероятностей и ее применения. 1975. Т.20. 1. С.134-140. |
| [3] | Утев С.А., Гринь А.Г. Нижние оценки для дисперсий сумм слабозависимых величин // Сибирский математический журнал. 1994. Т.35. 1. С.210-220. |
| [4] |
Bradley R. The central limit questions under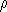 - mixing.-
Rocky Mountain J. 1987. V.17. 1. P.95 - 114.
- mixing.-
Rocky Mountain J. 1987. V.17. 1. P.95 - 114.
|
| [5] |
Гринь А.Г. Центральная предельная теорема для схем серий с
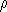 -перемешиванием. // Математические заметки. 1995. Т.57. В.6. С.842-850. -перемешиванием. // Математические заметки. 1995. Т.57. В.6. С.842-850.
|
| [6] |
Peligrad M. On the central limit theorem for 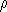 -
mixing sequences of random variables.- Annals of Probability,
1987. V.15. 4. P. 1387-1394.
-
mixing sequences of random variables.- Annals of Probability,
1987. V.15. 4. P. 1387-1394.
|
| [7] |
Утев С.А. Суммы случайных величин с 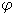 - перемешиванием //
Асимптотический анализ распределений случайных процессов. Новосибирск:
Наука. Сиб.отд-ние, 1989 (Тр. СОАН СССР, Ин-т математики. Т.13).
- перемешиванием //
Асимптотический анализ распределений случайных процессов. Новосибирск:
Наука. Сиб.отд-ние, 1989 (Тр. СОАН СССР, Ин-т математики. Т.13).
|
| [8] | Denker M. Uniform integrability and the central limit teorem for strongly mixing processes.- Dependence in Probability and Statistics (Ser. Progress in Probability and Statistics). Boston -Basel - Stuttgart: Birkhäuser, 1986. Р. 269 - 274. |