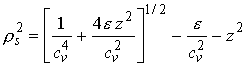
| Вестник ОмГУ | Выпуск | Тематика | Литература |
| Вестник Омского университета, 1999,
Вып. 1. С. 25-27. © Омский государственный университет, 1999 |
УДК 539.173 |
П.Н. Надточий
Омский государственный университет,
кафедра теоретической физики
644077, Омск, пр. Мира, 55-А
Получена 1 октября 1998 г.
| The reduced friction coefficient was calculated in the one-body and two-body mechanisms of nuclear dissipation for main fission coordinate. The mean time of descent from saddle to scission have been calculated within the stohactic approach based on the Langevin equations of the nuclear fission. The calculated results were compared with the experimental data. |
Среди многих вопросов, возникающих при описании деления ядер, одним из самых важных является вопрос о механизме ядерной вязкости. Двухтельный [1] или однотельный [2] механизм вязкости применим для описания свойств ядерной материи при делении ядер? Многие исследования, посвященные данному явлению [3,4], не позволили дать однозначного ответа.
Расчеты, о которых говорится в настоящей статье, были проведены в надежде добиться некоторой ясности в этом вопросе.
В данной работе вычислялось время спуска с седла, как одна из величин, непосредственно связаная со временем деления ядер, которое в свою очередь является критичным к механизму ядерной вязкости. Вычисление времени спуска было проведено на основе численного решения стохастических уравнений Ланжевена. Все расчеты проводились для возбужденных ядер, температура которых на барьере Т = 1,5 МэВ, что позволило не учитывать оболочечные эффекты и эффекты спаривания нуклонов. Такие условия ассимптотически приводят к квазиклассическим значениям характеристик ядра, которые могут быть рассчитаны в макроскопических подходах и моделях.
Для описания формы ядра была выбрана параметризация овалоидов Кассини [5]. В случае одномерной задачи, рассматриваемой в данной работе, уравнение поверхности в циллиндрических координатах будет иметь вид:
|
(1) |
где e-коллективная переменная, отвечающая за удлинение, а cv- масштабный фактор, зависящий от e через условие сохранения объема. При e = 0 рассматриваемое тело вращения есть сфера, с увеличением e она превращается в вытянутое тело овальной формы, у которого начиная с e = 0,5 появляется шейка. С дальнейшим увеличением e шейка утоньчается и при e = 1 ее толщина становится равной нулю. При проведении динамических расчетов удобно ввести вместо переменной e переменую b, равную половине расстояния между центрами масс будущих осколков:
|
(2) |
где R0-радиус начальной сферы.
В настоящее время одним из наиболее развивающихся в ядерной физике подходов является стохастический. В его основе лежит решение системы стохастических уравнений Ланжевена, которые записываются в виде:
|
(3) |
|
(4) |
Здесь ![]() -
обобщенная координата, в нашем случае это b;
а
-
обобщенная координата, в нашем случае это b;
а ![]() - сопряженный
ей импульс; V - потенциальная энергия; b - коэффициент затухания
коллективного движения, который находится как
отношение фрикционного коэффициента g
к массовому m; x(t)- случайная
сила со свойствами < x(t) > = 0, < x(t1)x(t2) > = 2Dd(t1-t2).
Предполагается выполненым соотношение
Эйнштейна D = gT, где T-
температура ядра, определяемая соотношением T
= (Eint/a)1/2, a-параметр
плотности уровней, a = A/10, Eint-внутреняя
энергия возбуждения ядра, определяемая из закона
сохранения энергии:
- сопряженный
ей импульс; V - потенциальная энергия; b - коэффициент затухания
коллективного движения, который находится как
отношение фрикционного коэффициента g
к массовому m; x(t)- случайная
сила со свойствами < x(t) > = 0, < x(t1)x(t2) > = 2Dd(t1-t2).
Предполагается выполненым соотношение
Эйнштейна D = gT, где T-
температура ядра, определяемая соотношением T
= (Eint/a)1/2, a-параметр
плотности уровней, a = A/10, Eint-внутреняя
энергия возбуждения ядра, определяемая из закона
сохранения энергии:
|
(5) |
где Ekin - кинетическая энергия коллективной степени свободы, а E*-полная энергия возбуждения ядра.
Массовый коэффициент вычислялся в приближении Вернера - Уилера [6]. И согласно [7] он вычисляется:
|
(6) |
где штрихи означают производную по z. Коэффициент A вычисляется по формуле
|
(7) |
Потенциальная энергия V апроксимировалась по методу, предложенному в работе [8], где она бралась в виде гладко сшитых между собой двух парабол и гиперболы.
Для описания диссипации кинетической энергии при делении ядра используется два механизма вязкости: двухтельный и однотельный. При двухтельном фрикционный коэффициент вычисляется по формуле из работы [7]:
|
(8) |
где штрихи означают производную по z, а значение параметра g0 = 0,02ґ10-21 МэВ с фм-3 взято из работы [9] При однотельном механизме вязкости фрикционный коэффициент вычислялся по формулам из [7]:
|
(9) |
где
|
(10) |
|
(11) |
где rm - массовая плотность ядра, v - средняя скорость нуклонов внутри ядра, Sw = pR2 - площадь перемычки, соединяющей два будущих осколка, a = pR/(zmax-zmin) - безразмерный параметр, R - радиус перемычки. Значение rmv = 1,026ґ10-22 МэВ с фм-4 было найдено в [10]. Для e < 0,5 вычисление фрикционного коэффициента производится по формуле (10), а после появления перемычки между осколками e > 0,5 по формуле (11). Формула (9) вводится для сглаживания зависимости фрикционного коэффициента от e.
Для начала расчета времени спуска tf необходимо было вычислить коэффициент затухания коллективного движения b. В данной работе этот коэффициент вычислялся в однотельном и двухтельном механизме вязкости. Его расчет привел к неожиданному результату. В работе [11] для описания множественности предразрывных частиц и вероятности деления ядер была постулирована следующая необычная зависимость от основной делительной координаты b: при b < 0,6 b = 2ґ1021c-1, а при b > 0,6 b линейно возрастает до 30ґ1021 с-1. Причем такая зависимость считалась универсальной для всех ядер. Результаты проведенных расчетов представлены на рис. 1.
При расчете времени спуска в качестве начальных условий на гребне выбирались: температура ядра T = 1,5МэВ, E* = 100 МэВ. Система уравнений Ланжевена решалась по разностной схеме [8]. Результаты расчета представлены на рис. 2.
В данной работе проводилось вычисление времени спуска с седла, и поэтому сопоставление с экспериментальными данными имеет смысл проводить только в области тяжелых ядер X > 0,75, у которых седловая точка близка по конфигурации к основному состоянию, и процесс деления состоит, по существу, из одного спуска. Если рассматривать область X > 0,75, то видно, что расчетная кривая с однотельным механизмом вязкости вплотную приближается к экспериментальным данным, а в области малых X существенно от них отличается, как этого и следовало ожидать. Расчеты с двухтельным механизмом вязкости приводят к явно заниженным результатам, к тому же время спуска оказалось практически не зависящим от ядра. Но следует отметить, что данные, представленные на рис. 2, не являются чисто экспериментальными. В эксперименте измеряется число испущенных нейтронов во время деления и на основе модельных представлений вычисляется время деления. Таким образом, данные о времени деления оказываются модельнозависимыми.
В других моделях, как отмечает автор [12], время деления оказывается больше, но тенденция его к уменьшению сохраняется.
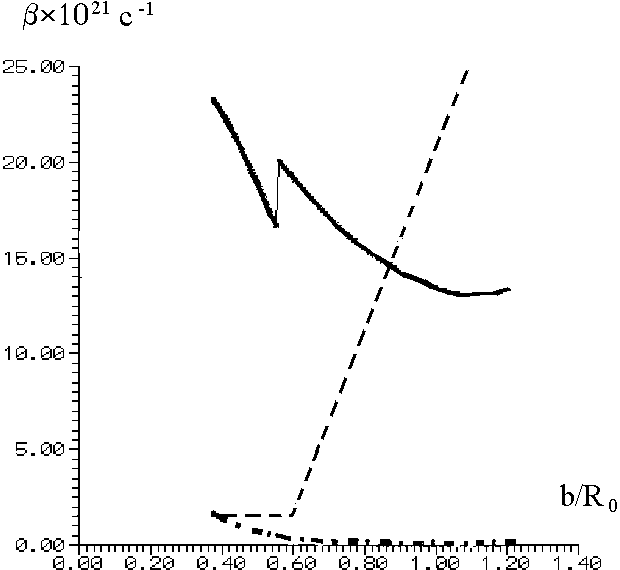 |
| Рис. 1. Зависимость коэффициента b от b/R0. Сплошной линией - данные для однотельной вязкости ядра 238U, штрих-пунктирной линией - для двухтельной вязкости ядра 238U, пунктирной линией - данные из работы [11]. |
В процессе проведенных расчетов был вычислен коэффициент b для однотельного и двухтельного механизмов диссипации. Его поведение оказалось существенно отличным от предполагаемого в работе [11], но неплохо согласующимся с экспериментальными данными.
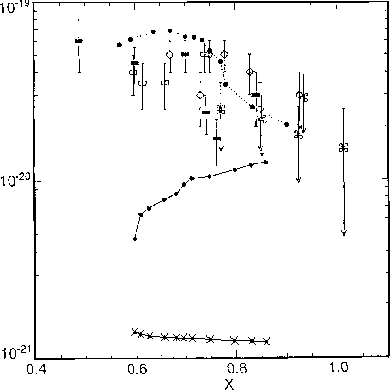 |
| Рис. 2. Зависимость полного времени деления (разные значки с ошибками) от параметра делимости X [12]. Теоретические кривые: соединенные линиями кружки - расчет времени спуска настоящей работы с однотельным механизмом вязкости, соединеные линиями крестики - с двухтельным, соединенные точками кружки - расчет наиболее вероятного времени деления из работы [11]. |
На основе полученных результатов можно сказать, что механизм однотельной вязкости позволяет более успешно описывать экспериментально полученные времена деления даже на основе столь простой модели. Для более обоснованных количественных выводов несомненно следует переходить к двумерной модели, включать испарение частиц, что позволит более детально сравнивать расчеты с экспериментальными данными.
Автор выражает глубокую благодарность Г.Д. Адееву за многочисленные полезные обсуждения и другую методическую помощь.
| [1] | Davies K.R.T., Sierk A.J., Nix J.R. // Phys. Rev. C13, 2385 (1976) |
| [2] | Blocki J., Boneh Y., Nix J.R., Randrup J., Robel M., Sierk A.J., Swiatecki W.J. // Ann. Phys. (N. Y.) 113, 330 (1978) |
| [3] | Адеев Г.Д., Гончар И.И., Пашкевич В.В., Писчасов Н.И., Сердюк О.И.// ЭЧАЯ. 1988. Т.19. Вып.6. С. 1229 - 1298. |
| [4] | Abe Y., Ayik S., Reinhard P.-G., Suraud E. // Phys. rep. 1996. V 275. Р. 49-196. |
| [5] | Ставинский В.С., Работнов Н.С., Серегин А.А. // Ядерная физика. 1968. Т. 7. С. 1051-1056. |
| [6] | Kelson I.// Phys. Rev. 1964. V. 136B. P. 1667. |
| [7] | Feldmeier H.// Rep. Prog. Phys. 1987. V. 50. P. 915-994. |
| [8] | Косенко Г.И.// Ядерная физика. 1993. Т. 56. Вып. 2. С. 77-86. |
| [9] | Косенко Г.И., Коляри И.Г., Адеев Г.Д.// Ядерная физика. 1997. Т.60. Вып. 3. С. 404-412. |
| [10] | Randrup J., Swiatecki W. J. // Annals of Physics. 1980. С. 193-226. |
| [11] | Гончар И.И. // ЭЧАЯ. 1995. Т. 26. С. 932-1000. |
| [12] | Иткис М.Г., Русанов А.Я. // ЭЧАЯ. 1998. Т.29. С. 389-488. |