
| Вестник ОмГУ | Выпуск | Тематика | Литература |
| Вестник Омского университета, 1999, Вып. 1. С. 19-21. © Омский государственный университет, 1999 |
УДК 519.48 |

А.В. Ющенко
Омский государственный университет, кафедра алгебры
644077, Омск, пр. Мира,55-A
Получена 3 ноября 1998 г.
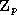 -forms of Lie algebra -forms of Lie algebra  ,
obtained by extension of diagonal form with single element,
are considered, and maximal diagonal ideals for some of such forms
are described. ,
obtained by extension of diagonal form with single element,
are considered, and maximal diagonal ideals for some of such forms
are described. |
В работе рассматриваются 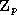 -формы алгебры Ли
-формы алгебры Ли  ,
получаемые расширением диагональной формы одним элементом,
и описываются максимальные диагональные идеалы для некоторого класса
таких форм.
,
получаемые расширением диагональной формы одним элементом,
и описываются максимальные диагональные идеалы для некоторого класса
таких форм.
Определение 1. Алгебры Ли 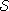 над
над 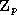 называется
называется 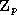 -формой
алгебры Ли
-формой
алгебры Ли  , если
, если 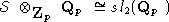 и
и 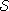 - конечномерный
- конечномерный 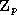 -модуль.
-модуль.
Зафиксируем базис 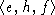 в
в 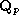 такой, что
такой, что  eh = pn e, fh = - pnf, ef=pd h.
eh = pn e, fh = - pnf, ef=pd h.
Далее всюду предполагается, что 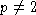 .
.
Предложение 1. Пусть 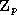 -форма
-форма
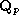 порождена элементами
порождена элементами 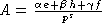 ,
e, h, f и
,
e, h, f и 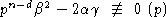 при
при 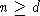 или
или 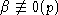 при n < d. Тогда существуют
элементы e', h', f' такие, что
при n < d. Тогда существуют
элементы e', h', f' такие, что 
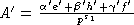
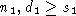
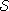 порождена элементами A', e', h', f', и
порождена элементами A', e', h', f', и
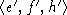 идеал в
идеал в 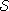 .
.
 Индукция по индексу подалгебры
Индукция по индексу подалгебры 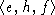 .
.
Если индекс 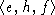 в
в 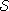 равен единице,
т.е.
равен единице,
т.е. 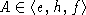 то s=0 и утверждение очевидно.
то s=0 и утверждение очевидно.
 ,
,
 ,
,
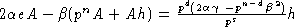 .
.
Пусть 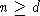 и
и 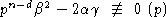 .
Тогда
.
Тогда 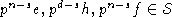 ,
Eсли d<s, то
,
Eсли d<s, то 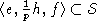 - подалгебра меньшего индекса.
- подалгебра меньшего индекса.
Пусть n < d и 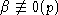 .
Тогда аналогично получим, что
.
Тогда аналогично получим, что 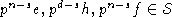 .
Если n<s то
.
Если n<s то 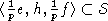 - подалгебра меньшего индекса.
- подалгебра меньшего индекса.
Следовательно, в дальнейшем можно рассматривать 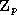 -формы,
определенные следующим образом:
-формы,
определенные следующим образом:
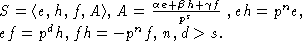 |
(1) |
Лемма 1. Пусть 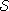 -
-
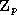 -форма алгебры Ли
-форма алгебры Ли  определенная (1),
определенная (1), 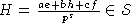 .
.
1) Если 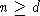 ,
,
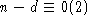 и
и 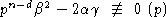 ,
то H-полупростой
,
то H-полупростой 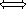
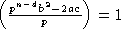 .
.
2) Если 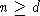 ,
, 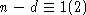 и
и 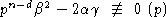 , то H-не является полупростым.
, то H-не является полупростым.
3) Если 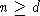 ,
, 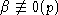 ,
то H-полупростой.
,
то H-полупростой.
 1)
1) 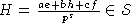 - полупростой.
Заметим, что
- полупростой.
Заметим, что 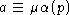 ,
,
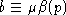 ,
,
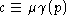 и
и
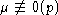 .
E - собственный вектор. E= xe+yh+zf,
.
E - собственный вектор. E= xe+yh+zf,
 .
Получаем систему линейных уравнений
.
Получаем систему линейных уравнений
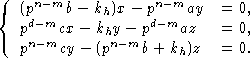 |
(2) |
Она имеет ненулевое решение, следовательно, ее определитель равен нулю.
Вычисляем его: (p2(n-m)b2 - kh2)kh - 2 pn+d-2mac kh=0.
Так как 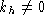 ,
то p2(n-m)b2 - kh2 - 2 pn+d-2mac =0.
Разделим на pn+d-2m, получим
pn-db2 - 2 ac =k2, где kh= p(n+d)/2-mk.
То есть pn-db2 - 2 ac квадрат в
,
то p2(n-m)b2 - kh2 - 2 pn+d-2mac =0.
Разделим на pn+d-2m, получим
pn-db2 - 2 ac =k2, где kh= p(n+d)/2-mk.
То есть pn-db2 - 2 ac квадрат в 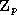 и из условия
и из условия
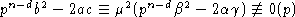 , получаем
, получаем 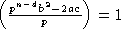 .
.
Обратно,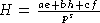 .Положим p2tb2-2ac=k2, t=(n-d)/2,
и
.Положим p2tb2-2ac=k2, t=(n-d)/2,
и 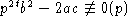 ,
тогда
,
тогда
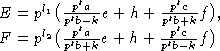 |
(3) |
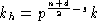 .
l1, l2 такие, что
.
l1, l2 такие, что 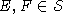 .
.
2) 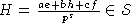 - полупростой. Аналогично п.1) вычисляем определитель системы (2), получаем, что
(pn-db2 - 2 ac)p =k2, где
- полупростой. Аналогично п.1) вычисляем определитель системы (2), получаем, что
(pn-db2 - 2 ac)p =k2, где 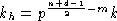 .
Следовательно,
.
Следовательно, 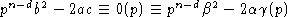 - противоречие.
- противоречие.
3) n<d, 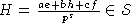 - полупростой. Аналогично п.1) вычисляем определитель системы (2),
получаем, что b2 -2 pn-dac должно быть ненулевым квадратом в
- полупростой. Аналогично п.1) вычисляем определитель системы (2),
получаем, что b2 -2 pn-dac должно быть ненулевым квадратом в 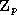 ,
но так как n<d и
,
но так как n<d и 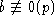 , это всегда верно.
, это всегда верно.
Пусть J подалгебра в S, 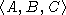 - ее базис. Обозначим через
- ее базис. Обозначим через 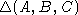 определитель матрицы перехода от
определитель матрицы перехода от 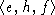 к
к 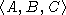 .
Тогда легко проверяется, что
.
Тогда легко проверяется, что 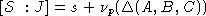 .
.
 Лемма 2 Пусть
Лемма 2 Пусть 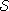 -
-
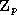 -форма алгебры Ли
-форма алгебры Ли  определенная (1) и
определенная (1) и 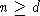
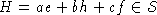 - полупростой элемент, E, F -
собственные вектора для H. Тогда
- полупростой элемент, E, F -
собственные вектора для H. Тогда 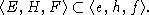 .
.
Если 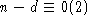 ,
то возьмем t=(n-d)/2,
в случае
,
то возьмем t=(n-d)/2,
в случае 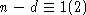 t=(n-d+1)/2.
t=(n-d+1)/2.
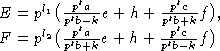
- собственные вектора для H,
l1, l2 - минимальные, такие что
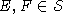 .
.
 .
Положим
.
Положим 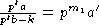 ,
,
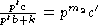 ,
,
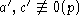 .
.
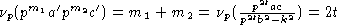 .
Так как
.
Так как  ,
то либо
,
то либо 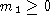 ,
либо
,
либо  .
.
Рассмотрим случай 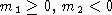 .
Пусть m2'=-m2, тогда
.
Пусть m2'=-m2, тогда
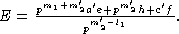 Если m2'-l1 > 0, то из условия
Если m2'-l1 > 0, то из условия 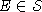 получим
систему сравнений
получим
систему сравнений
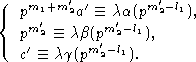
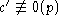 имеем
имеем 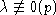 .
Так как m1+m2' > 0 и m2'> 0, то
.
Так как m1+m2' > 0 и m2'> 0, то 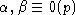 ,
получаем противоречие с условием
,
получаем противоречие с условием 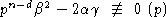 .
.
Следовательно, 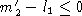 и
и 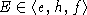 ,
аналогично доказывается, что
,
аналогично доказывается, что 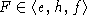 .
.
Случай 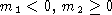 рассматриваюся так же.
рассматриваюся так же.
Определение 2 Подалгебра J в S
называется диагональной, если существуют полупростой 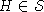 и E, F - собственные для H, такие, что
и E, F - собственные для H, такие, что 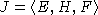
 1) Из леммы 2 следует, что достаточно рассмотреть случай,
когда полупростой элемент вида
1) Из леммы 2 следует, что достаточно рассмотреть случай,
когда полупростой элемент вида 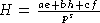 входит в диагональный базис.
Из условия
входит в диагональный базис.
Из условия 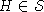 получаем
получаем
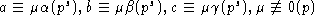 .
По лемме 1
.
По лемме 1 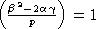 ,
следовательно,
,
следовательно, 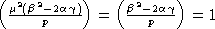 .
.
Пусть 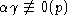 ,
тогда
,
тогда 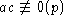 и
и
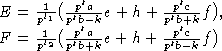
- собственные вектора H.
Пусть l1>0, тогда из условия 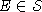 получим систему сравнений
получим систему сравнений
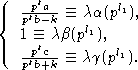
Из второго сравнения 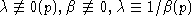 , и
если t >0, то
, и
если t >0, то 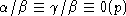 - противоречие.
Следовательно, либо t=0, либо
- противоречие.
Следовательно, либо t=0, либо  и l1=l2=0.
и l1=l2=0.
Пусть t=0, тогда система сравнений примет вид
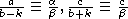 .
Перемножая эти сравнения и пользуясь условием 2ac=b2-k2, получим
.
Перемножая эти сравнения и пользуясь условием 2ac=b2-k2, получим
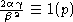 или
или 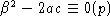 - противоречие.
Таким образом, если
- противоречие.
Таким образом, если 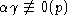 ,
то l1=l2=0.
,
то l1=l2=0.
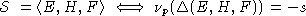 .
Вычисляем
.
Вычисляем  ,
получим
,
получим 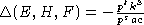 .
Так как
.
Так как 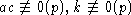 ,
то
,
то 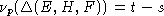 , следовательно, t=0.
, следовательно, t=0.
Положим теперь 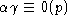 .
Тогда из условия
.
Тогда из условия 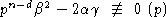 следует, что t=0.
следует, что t=0. 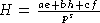 - полупростой элемент, 2ac=b2 -k2,
так как
- полупростой элемент, 2ac=b2 -k2,
так как 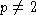 ,
то либо
,
то либо 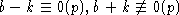 ,
либо
,
либо  .
.
Рассмотрим случай 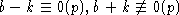 .
Тогда
.
Тогда
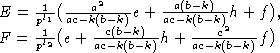
- собственные вектора H. Заметим, что 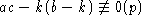 .
.
Пусть 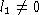 ,
тогда из условия
,
тогда из условия 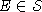 получим систему сравнений:
получим систему сравнений:
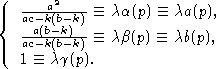
Из третьего сравнения 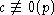 ,
значит,
,
значит, 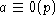 .
Из второго:
.
Из второго: 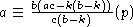 ,
следовательно,
,
следовательно, 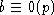 и
и 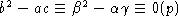 - противоречие. Таким образом, l1 =0, аналогично доказывается l2=0.
- противоречие. Таким образом, l1 =0, аналогично доказывается l2=0.
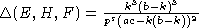 .
Cледовательно,
.
Cледовательно, 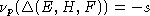 и S диагональная. Случай
и S диагональная. Случай  разбирается полностью аналогично.
разбирается полностью аналогично.
2) Возьмем H полупростой, предположим что  и E,F определены формулами:
и E,F определены формулами:
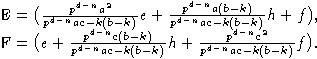 |
(4) |
Проверим, что E,H,F - базис S.
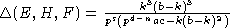 ,
так как
,
так как 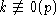 и
и  то
то 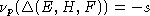 ,
то есть E,H,F образуют базис S.
,
то есть E,H,F образуют базис S.
В случае  надо воспользоваться формулами:
надо воспользоваться формулами:
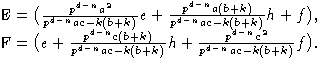 |
(5) |
Выясним, когда элемент u1e+u2h+u3f принадлежит
идеалу 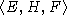 .
.
xE+yH+zF=u1e+u2h+u3f.
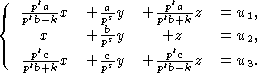
При решении системы получим:
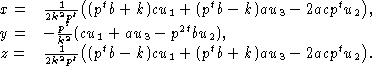 |
(6) |
Предложение 2. Пусть S - недиагональная
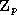 - форма алгебры Ли
- форма алгебры Ли
 , определенная (2),
, определенная (2),
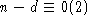 t=(n-d+1)/2.
t=(n-d+1)/2.
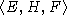 - максимальный диагональный идеал.
Тогда
- максимальный диагональный идеал.
Тогда 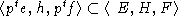 и
и  ,
,
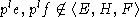
 Пусть t =0, тогда из предыдущей теоремы
и леммы 1 получаем, что в S нет диагональных идеалов
вида
Пусть t =0, тогда из предыдущей теоремы
и леммы 1 получаем, что в S нет диагональных идеалов
вида  .
Пусть теперь
.
Пусть теперь  ,
тогда
,
тогда 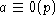 .
Из формул (6), для e=xE+yH+zF, получаем
.
Из формул (6), для e=xE+yH+zF, получаем
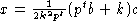 ,
,
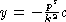 ,
,
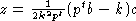 .
.
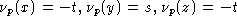 .
Следовательно,
.
Следовательно, 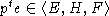 и
и
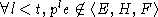 .
То, что
.
То, что  , проверяется аналогично.
, проверяется аналогично.
Теорема 2. Пусть S - недиагональная 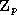 -форма
алгебры Ли
-форма
алгебры Ли  , определенная (1),
, определенная (1),
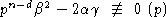
1) n = d,  ,
тогда в S единственный максимальный диагональный идеал
,
тогда в S единственный максимальный диагональный идеал 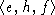 .
.
2) n > d, 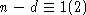 ,
тогда в S единственный максимальный диагональный идеал
,
тогда в S единственный максимальный диагональный идеал 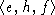 .
.
3) n > d, 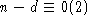 ,
,
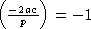 , тогда в S все
максимальные диагональные идеалы имеют вид либо
, тогда в S все
максимальные диагональные идеалы имеют вид либо 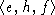 ,
либо
,
либо  - полупростой, E, F -
собственные для H.
- полупростой, E, F -
собственные для H.
Причем, если  другой полупростой элемент, тогда
другой полупростой элемент, тогда 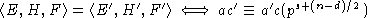 .
.
 1) и 2) непосредственно следуют из лемм 1 и 2.
1) и 2) непосредственно следуют из лемм 1 и 2.
3) Возьмем полупростой элемент 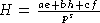 ,
рассмотрим соответствующий идеал
,
рассмотрим соответствующий идеал 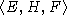 .
Из предложения 2 получаем
.
Из предложения 2 получаем 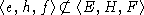 .
Следовательно,
.
Следовательно, 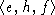 - максимальный диагональный идеал в S.
- максимальный диагональный идеал в S.
Далее, пусть  другой полупростой элемент,
другой полупростой элемент, 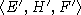 - соответствующий ему идеал. Выясним, когда
- соответствующий ему идеал. Выясним, когда 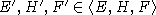 .
.
E'= xE+yH+zF.
Из (6) получаем 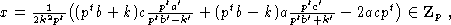 аналогично
аналогично 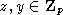 ,
т.е.
,
т.е. 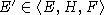 .
Те же рассуждения проводим для
.
Те же рассуждения проводим для  .
Предварительно заметим, что
.
Предварительно заметим, что 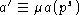 ,
,
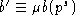 ,
,
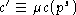 ,
,
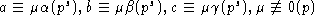 .
.
H'=xE+yH+zF.
Из формул (6) получим 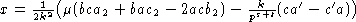 ,
аналогично вычисляем z.
Таким образом,
,
аналогично вычисляем z.
Таким образом, 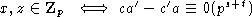 .
.
 .
.
Следовательно, 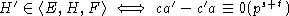 ,
симметрично получаем
,
симметрично получаем 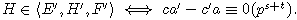 .
.
| [1] | Джекобсон Н.Алгебры Ли. M.: Мир, 1964. |