| Вестник ОмГУ | Выпуск | Тематика | Литература |
| Вестник Омского
университета, 1998, Вып. 2. С. 21-24 © Омский государственный университет, 1998 |
УДК 519.1 |
Д.И. Яковенко
Омский государственный университет,
кафедра алгебры
644077, Омск, пр. Мира, 55-А
Получена 15 мая 1997 г.
| We find a number of necklaces from m beads of q kinds, and besides the necklaces are considered to be equivalent in case, if they are combining with turnings or axises' symmetry. |
Рассмотрим следующую комбинаторную задачу.
Задача 1. Имеется ![]() сортов бусин (каждый сорт в изобилии). Сколько
ожерелий из
сортов бусин (каждый сорт в изобилии). Сколько
ожерелий из ![]() бусин можно
составить?
бусин можно
составить?
Эта задача имеет две постановки. Во-первых, можно считать, что ожерелья равны тогда и только тогда, когда одно получается из другого поворотом. Во-вторых, можно считать равными два ожерелья, полученные друг из друга поворотом, осевой симметрией или их композицией.
"Задача об ожерельях" в первой постановке
хорошо известна алгебраистам. Еще К.Гаусс вывел
формулу, которая дает число неприводимых
нормированных многочленов над конечным полем
[1]. В XX веке Е.Витт нашел число
базисных слов длины ![]() в
алфавите из
в
алфавите из ![]() букв в
свободной алгебре Ли. И обе эти формулы совпадают
с решением задачи об ожерельях! При этом
доказательство формулы Витта такое же, как
решение комбинаторной задачи об ожерельях [2]. В качестве следствия из формулы Витта
легко вывести малую теорему Ферма и ее обобщение
- теорему Эйлера.
букв в
свободной алгебре Ли. И обе эти формулы совпадают
с решением задачи об ожерельях! При этом
доказательство формулы Витта такое же, как
решение комбинаторной задачи об ожерельях [2]. В качестве следствия из формулы Витта
легко вывести малую теорему Ферма и ее обобщение
- теорему Эйлера.
В нашей работе рассматривается другой вариант этой задачи.
Задача 2. Найти число ожерелий из ![]() бусин
бусин ![]() сортов,
если имеется
сортов,
если имеется ![]() бусин 1-го
сорта,
бусин 1-го
сорта, ![]() бусин 2-го сорта,...,
бусин 2-го сорта,..., ![]() бусин
бусин ![]() -го
сорта. Это число обозначается
-го
сорта. Это число обозначается ![]() . При этом равными считаются ожерелья,
полученные друг из друга с помощью поворота или
отражения.
. При этом равными считаются ожерелья,
полученные друг из друга с помощью поворота или
отражения.
Мы решили эту задачу, применяя лемму Бернсайда [1].
Лемма Бернсайда. Для любой группы
перестановок имеет место равенство 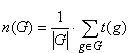 , где
, где ![]() - число орбит
группы
- число орбит
группы ![]() ,
, ![]() - число неподвижных точек перестановки
- число неподвижных точек перестановки ![]() .
.
В качестве следствия из формулы для ![]() получено решение задачи 1 во второй
постановке.
получено решение задачи 1 во второй
постановке.
Перейдем к решению задачи 2. Эта задача
равносильна следующей задаче: сколькими
различными способами можно раскрасить вершины
правильного ![]() -угольника в
-угольника в ![]() цветов, чтобы было
цветов, чтобы было ![]() вершин 1-го цвета,
вершин 1-го цвета, ![]() вершин 2-го цвета,...,
вершин 2-го цвета,..., ![]() вершин
вершин ![]() -го цвета. Здесь два способа
раскраски неотличимы, если один из них можно
получить из другого, применяя к
-го цвета. Здесь два способа
раскраски неотличимы, если один из них можно
получить из другого, применяя к ![]() -угольнику либо преобразование
вращения, либо симметрии относительно осей.
-угольнику либо преобразование
вращения, либо симметрии относительно осей.
Пусть ![]() - множество
всевозможно раскрашенных
- множество
всевозможно раскрашенных ![]() -угольников.
-угольников.
![]() - группа симметрий
- группа симметрий ![]() -угольника, состоящая из
-угольника, состоящая из ![]() преобразований. Группа
преобразований. Группа ![]() естественным образом
определяет группу перестановок на множестве
естественным образом
определяет группу перестановок на множестве ![]() . Именно, если
. Именно, если ![]() - некоторое преобразование симметрии,
то каждому многоугольнику из
- некоторое преобразование симметрии,
то каждому многоугольнику из ![]() можно сопоставить некоторый
многоугольник, который получается из первого
симметрией
можно сопоставить некоторый
многоугольник, который получается из первого
симметрией ![]() . Это
соответствие является перестановкой на
множестве
. Это
соответствие является перестановкой на
множестве ![]() , которую будем
обозначать
, которую будем
обозначать ![]() . Группу всех
таких перестановок множества
. Группу всех
таких перестановок множества ![]() , определяемых перестановками из
, определяемых перестановками из ![]() , будем обозначать
, будем обозначать ![]() .
.
При подсчeте числа ожерелий два многоугольника
считаются одинаковыми, если один можно перевести
в другой какой-то перестановкой из ![]() , то есть они содержатся в одной орбите
группы
, то есть они содержатся в одной орбите
группы ![]() , действующей на
множестве
, действующей на
множестве ![]() . Таким образом,
для того чтобы определить число геометрически
различимых способов раскраски вершин
. Таким образом,
для того чтобы определить число геометрически
различимых способов раскраски вершин ![]() -угольника (число ожерелий), нужно найти
количество орбит группы
-угольника (число ожерелий), нужно найти
количество орбит группы ![]() на
множестве
на
множестве ![]() . Количество орбит
можно найти по лемме Бернсайда, для этого
необходимо определить число неподвижных точек
каждой перестановки из
. Количество орбит
можно найти по лемме Бернсайда, для этого
необходимо определить число неподвижных точек
каждой перестановки из ![]() .
.
Рассмотрим сначала повороты. Если ![]() общий делитель чисел
общий делитель чисел ![]() , то поворот
, то поворот ![]() на
угол
на
угол ![]() оставляет
неподвижными ожерелья, состоящие из
оставляет
неподвижными ожерелья, состоящие из ![]() одинаковых кусков длины
одинаковых кусков длины ![]() . Каждый кусок состоит из
. Каждый кусок состоит из ![]() бусин 1-го сорта,
бусин 1-го сорта, ![]() бусин 2-го сорта,...,
бусин 2-го сорта,..., ![]() бусин
бусин ![]() -го сорта, поэтому число
неподвижных точек для этого поворота равно числу
способов расставить эти бусины на
-го сорта, поэтому число
неподвижных точек для этого поворота равно числу
способов расставить эти бусины на ![]() местах, то есть
местах, то есть ![]() ,
где
,
где ![]() - полиномиальные
коэффициенты [5].
- полиномиальные
коэффициенты [5].
Рассмотрим поворот ![]() на угол
на угол ![]() , где
, где ![]() . Этот поворот имеет такое же
количество неподвижных точек, сколько
. Этот поворот имеет такое же
количество неподвижных точек, сколько ![]() , если
, если ![]() взаимно
просто с
взаимно
просто с ![]() . Количество чисел,
не превосходящих
. Количество чисел,
не превосходящих ![]() и взаимно
простых с
и взаимно
простых с ![]() , - это функция
Эйлера
, - это функция
Эйлера ![]() . Обозначим через
. Обозначим через ![]() cумму
cумму ![]() по
всем поворотам, тогда
по
всем поворотам, тогда ![]() , где
, где ![]() пробегает множество всех
общих делителей чисел
пробегает множество всех
общих делителей чисел ![]() .
.
Рассмотрим симметрии относительно осей.
1 случай: ![]() нечeтно. В этом случае симметричные
ожерелья существуют только тогда, когда среди
чисел
нечeтно. В этом случае симметричные
ожерелья существуют только тогда, когда среди
чисел ![]() только одно нечeтно.
Пусть
только одно нечeтно.
Пусть ![]() нечeтно,
нечeтно, ![]() - симметрия относительно оси,
проходящей через некоторую вершину. Тогда
неподвижными будут ожерелья, симметричные
относительно оси,проходящей через бусину 1-го
сорта. По одну сторону от оси находится
- симметрия относительно оси,
проходящей через некоторую вершину. Тогда
неподвижными будут ожерелья, симметричные
относительно оси,проходящей через бусину 1-го
сорта. По одну сторону от оси находится ![]() бусин, из них
бусин, из них ![]() бусин 1-го сорта,
бусин 1-го сорта, ![]() бусин 2-го сорта,...,
бусин 2-го сорта,..., ![]() бусин
бусин ![]() -го сорта, поэтому
-го сорта, поэтому 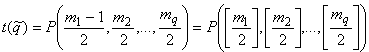 , где
, где ![]() - целая часть
числа
- целая часть
числа ![]() . Такое же количество
неподвижных точек имеет каждая из
. Такое же количество
неподвижных точек имеет каждая из ![]() перестановок, соответствующих таким
симметриям.
перестановок, соответствующих таким
симметриям.
Обозначим через ![]() cумму
cумму ![]() по всем отражениям, тогда
по всем отражениям, тогда 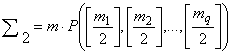
2 случай: ![]() чeтно. Ожерелья, симметричные относительно оси,
проходящей между бусинами, существуют только в
том случае, если все
чeтно. Ожерелья, симметричные относительно оси,
проходящей между бусинами, существуют только в
том случае, если все ![]()
![]() чeтны. Ожерелья, симметричные
относительно оси, проходящей через две бусины,
существуют только в двух случаях: все
чeтны. Ожерелья, симметричные
относительно оси, проходящей через две бусины,
существуют только в двух случаях: все ![]()
![]() чeтны или ровно
два из них нечeтны. a) Для определeнности будем
считать, что
чeтны или ровно
два из них нечeтны. a) Для определeнности будем
считать, что ![]() и
и ![]() нечeтны, остальные
нечeтны, остальные ![]() четны. Пусть
четны. Пусть ![]() -
симметрия относительно некоторой оси,
проходящей через противоположные вершины.
Неподвижными точками для
-
симметрия относительно некоторой оси,
проходящей через противоположные вершины.
Неподвижными точками для ![]() будут ожерелья, симметричные относительно оси,
проходящей через бусины 1-го и 2-го сортов. По одну
сторону от оси находится
будут ожерелья, симметричные относительно оси,
проходящей через бусины 1-го и 2-го сортов. По одну
сторону от оси находится ![]() бусин, из них
бусин, из них ![]() бусин 1-го
сорта,
бусин 1-го
сорта, ![]() - 2-го сорта,
- 2-го сорта, ![]() - i-го сорта
- i-го сорта ![]() . Учитывая, что бусины 1-го и 2-го сорта
можно поменять местами, получим
. Учитывая, что бусины 1-го и 2-го сорта
можно поменять местами, получим ![]() .
.
Таких симметрий ![]() ,
поэтому
,
поэтому 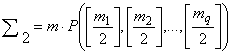 .
.
б) Все ![]() чeтны. Если
чeтны. Если ![]() - симметрия относительно
оси, проходящей через две вершины, то
неподвижными точками для
- симметрия относительно
оси, проходящей через две вершины, то
неподвижными точками для ![]() будут симметричные ожерелья, у которых две
бусины
будут симметричные ожерелья, у которых две
бусины ![]() -го сорта расположены
на этой оси
-го сорта расположены
на этой оси ![]() . Их
. Их ![]() .
.
Таких симметрий ![]() .
.
Если ![]() -
симметрия относительно оси, проходящей между
бусинами, то
-
симметрия относительно оси, проходящей между
бусинами, то ![]() . Таких
симметрий также
. Таких
симметрий также ![]() . Значит,
. Значит, 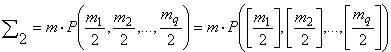 .
.
Итак, в случаях 1, 2а и 2б получились
одинаковые формулы для вычисления ![]() , где сумма берeтся по всем отражениям:
, где сумма берeтся по всем отражениям: 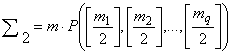
По лемме Бернсайда 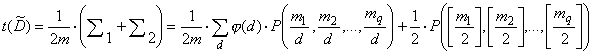 .
.
Если среди чисел ![]()
![]() более двух нечeтных, то нет
симметричных ожерелий, и
более двух нечeтных, то нет
симметричных ожерелий, и ![]() .
.
Итак, если среди ![]() не более
двух нечeтных, то
не более
двух нечeтных, то
|
(1) |
Если среди чисел ![]() более
двух нечeтных, то
более
двух нечeтных, то
|
(2) |
(здесь ![]() пробегает
множество всех общих делителей чисел
пробегает
множество всех общих делителей чисел ![]() ).
).
Рассмотрим несколько примеров и теоретико-числовых следствий полученных формул.
Пример 1. Число ожерелий из ![]() различных бусин
различных бусин ![]()
![]() .
.
Пример 2. Число ожерелий из ![]() синих и
синих и ![]() красных
бусин равно
красных
бусин равно
|
(3) |
(здесь ![]() для любого
для любого ![]() ).
).
Следствие 1. Для полимиальных
коэффициентов справедливо сравнение ![]() . Оно получается из формулы (1), если
. Оно получается из формулы (1), если ![]() .
.
Следствие 2. Из формулы для числа
ожерелий можно получить известное тождество для
функции Эйлера [6], полагая n = 0 в
формуле (3): 
Задачу 1 во второй постановке можно решить тем
же методом, что и задачу 2. Но можно найти число
ожерелий ![]() из
из ![]() бусин
бусин ![]() сортов
(число бусин каждого сорта неограничено),
суммируя
сортов
(число бусин каждого сорта неограничено),
суммируя ![]() по всем
упорядоченным разбиениям числа
по всем
упорядоченным разбиениям числа ![]() на
на ![]() слагаемых:
слагаемых: ![]() ,
, ![]() . В
зависимости от четности
. В
зависимости от четности ![]() возникает два случая. Для нечетного
возникает два случая. Для нечетного ![]() все разбиения можно распределить на
две группы:
все разбиения можно распределить на
две группы:
1) разбиения, в которых одно слагаемое нечетно;
2) разбиения, в которых число нечетных
слагаемых больше 1. Соответственно этому ![]() находится по формуле (1) или (2).
находится по формуле (1) или (2).
Сложим числа ![]() по всем
разбиениям
по всем
разбиениям ![]() , изменим порядок
суммирования и воспользуемся формулой:
, изменим порядок
суммирования и воспользуемся формулой:
|
(4) |
где суммирование распространяется по
всем упорядоченным разбиениям ![]() на
на ![]() слагаемых:
слагаемых: ![]() [3] (c. 9). Если
[3] (c. 9). Если ![]() нечетно, то
нечетно, то ![]() . Cуммируя числа
. Cуммируя числа ![]() по
всем разбиениям c нечетным
по
всем разбиениям c нечетным ![]() и
снова применяя (4), получим
и
снова применяя (4), получим ![]() .
Умножая это число на
.
Умножая это число на ![]() ,
получим
,
получим 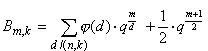 , если
, если ![]() нечетно.
нечетно.
Аналогично получается формула: 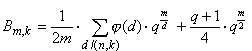 , если m четно.
, если m четно.
Автор выражает благодарность профессору Г.П.Кукину за постановку задачи и руководство работой.
| [1] | Кострикин А.И. Введение в алгебру. M.: Наука, 1977. |
| [2] | Ширшов А.И. О свободных кольцах Ли // Матем. сб. 1958. T. 45. N2. С. 113 - 122. |
| [3] | Комбинаторный анализ. Задачи и упражнения / Под ред. К.А.Рыбникова. M.: Наука, 1982. |
| [4] | Калужнин Л.А., Сущанский В.И. Преобразования и перестановки. М.: Наука, 1979. |
| [5] | Балашова Н.А., Кукин Г.П. Комбинаторика. Омск, 1992. |
| [6] | Виноградов И.М. Основы теории чисел. М.: Наука, 1965. |