 |
(1) |
| Вестник ОмГУ | Выпуск | Тематика | Литература |
| Вестник Омского университета, 1998,
Вып. 1. С. 22-25. © Омский государственный университет, 1998 |
УДК 539.612 |
М.В.Мамонова, В.В.Прудников
Омский государственный университет, кафедра теоретической физики
644077, Омск, пр. Мира,55-A
Получена 20 ноября 1997 г.
| Тне мethod of calculation of electron work function was eleborated in frame of electron density functional method for a number of simple and transition metals. The Heine-Abarenkov pseudopotential was applied for description of electron-ion interaction. The consideration of gradient corrections on inhomogeneous of electron density near surface and effects of displacement surface ionic plane were carried out. |
Одной из важных поверхностных характеристик является работа выхода электрона с поверхности металла. Сложность теоретического описания и сопоставления результатов расчета работы выхода с экспериментальными значениями по сравнению с подобной задачей для поверхностной энергии металлов заключается в наблюдаемом на эксперименте малом относительном изменении величины работы выхода для всего ряда металлов. Так, молибден обладает наибольшим значением поверхностной энергии, которая почти в двадцать раз превышает значение поверхностной энергии калия, в то время как значения работы выхода для них отличаются всего в два раза. До сих пор удовлетворительного согласия расчетных и экспериментальных результатов для работы выхода не было получено.
В предлагаемой работе в рамках метода функционала плотности проведен расчет работы выхода для ряда металлов. Исследованы влияния различных приближений, учитывающих дискретность кристаллической структуры и неоднородность электронного газа в поверхностном слое металлов.
Работа выхода определяется как минимальная энергия, необходимая для удаления электрона из объема твердого тела. Ее природа связана с существованием потенциального барьера вблизи поверхности металла. Величина работы выхода определяется разностью высоты потенциального барьера и химического потенциала:
 |
(1) |
Величину потенциала дипольного электрического слоя VD, действующего на электрон вблизи поверхности в рамках модели "желе", можно получить из уравнения Пуассона:
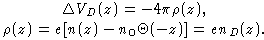 |
(2) |
В результате
 |
(3) |
Тогда высота дипольного потенциального барьера D0 в модели "желе" определяется выражением:
 |
(4) |
Распределение электронной плотности n(z) находится как функция, обеспечивающая минимум функционала полной энергии неоднородной системы.
Таблица 1
 (эрг/см2)
и работы выхода W(эВ) для ряда металлов
в модели псевдопотенциала Ашкрофта с учетом градиентных поправок
для наиболее плотноупакованных граней
(эрг/см2)
и работы выхода W(эВ) для ряда металлов
в модели псевдопотенциала Ашкрофта с учетом градиентных поправок
для наиболее плотноупакованных граней
| Металл | Величина | Градиентная поправка 2-го порядка | Град.поправка 4-го порядка к кин.эн. | Град.поправка 4-го порядка к обм.-кор.эн. |
| Na |  |
267 | 300 | 374 |
| (ОЦК) | W | 2.63 | 3.1 | 3.8 |
| K |  |
151 | 166 | 196 |
| (ОЦК) | W | 2.07 | 2.38 | 2.87 |
| Al |  |
941 | 1165 | 1860 |
| (ГЦК) | W | 3.25 | 4.2 | 6.3 |
| Cu |  |
872 | 1104 | 1798 |
| (ГЦК) | W | 3.98 | 4.95 | 7.07 |
| Fe |  |
635 | 1043 | 2394 |
| (ОЦК) | W | 3.44 | 4.56 | 7.31 |
| Cr |  |
641 | 1034 | 2334 |
| (ОЦК) | W | 3.5 | 4.57 | 7.27 |
Примечание. Подчеркнуты значения, наиболее соответствующие эксперименту.
При практических расчетах используется метод пробных функций, когда распределение электронной плотности n(z) выбирается в виде решения линеаризованного уравнения Томаса-Ферми:
 |
(5) |
где n0 - объемная электронная плотность;
 - вариационный параметр, определяемый при минимизации
функционала полной энергии неоднородной системы.
Тогда после интегрирования (4) получаем, что
- вариационный параметр, определяемый при минимизации
функционала полной энергии неоднородной системы.
Тогда после интегрирования (4) получаем, что
 |
(6) |
Учтем дискретное распределение заряда ионов. Следуя работе [1}, запишем дополнительный вклад к потенциальному барьеру за счет электрон-ионного взаимодействия в виде:
 |
(7) |
где
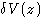 имеет смысл среднего по плоскостям от
суммы потенциалов ионов за вычетом потенциала полубесконечного однородного
положительного фона.
Так как выражение (7) однородно относительно ne, то
ne - можно считать
равной поверхностной плотности заряда, индуцированной слабым электрическим
полем с напряженностью Ez в полубесконечной модели однородного фона:
имеет смысл среднего по плоскостям от
суммы потенциалов ионов за вычетом потенциала полубесконечного однородного
положительного фона.
Так как выражение (7) однородно относительно ne, то
ne - можно считать
равной поверхностной плотности заряда, индуцированной слабым электрическим
полем с напряженностью Ez в полубесконечной модели однородного фона:
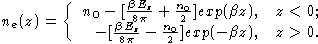 |
(8) |
Для вычисления поправки на электрон-ионное взаимодействие воспользуемся широко применяемым в физике металлов псевдопотенциалом Хейне-Абаренкова:
 |
(9) |
Таблица 2
 и
и 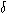 ,
работы выхода
,
работы выхода  (эВ)
с учетом и W(эВ) без учета релаксации.
(эВ)
с учетом и W(эВ) без учета релаксации.| Металл | Z | Wэксп, эВ | Rm, ат.ед. | V0, ат.ед. |  ат.ед. ат.ед. |
 ат.ед. ат.ед. |
W, эВ |  эВ эВ |
| Na (ОЦК) | 1 | 2.35 | 2.7 | 0.326 | 0.813 | 0.119 | 2.59 | 1.99 |
| K (ОЦК) | 1 | 2.137 | 2.5 | 0.087 | 0.679 | 0.145 | 2.13 | 1.66 |
| Al (ГЦК) | 3 | 4.24 | 1.2 | 0.19 | 1.151 | 0.052 | 4.25 | 2.85 |
| Cu (ГЦК) | 2 | 4.98 | 1.4 | 0.603 | 0.993 | 0.095 | 7.16 | 4.93 |
| Fe (ОЦК) | 4 | 4.31 | 1.2 | 0.475 | 1.149 | 0.064 | 7.24 | 4.43 |
| Cr (ОЦК) | 4 | 4.58 | 1.3 | 0.53 | 1.137 | 0.065 | 7.18 | 4.44 |
При условии V0=0 потенциал Хейне-Абаренкова переходит в выражение
для другого известного псевдопотенциала Ашкрофта.
Для 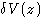 при -d<z<0 нами было получено следующее выражение:
при -d<z<0 нами было получено следующее выражение:
 |
(10) |
Проводя суммирование по ионным плоскостям с
z=-(i+d/2),i=1,2,...
и воспользовавшись периодичностью потенциала
 ,
из (7) получим
,
из (7) получим

| (11) |
Учет эффектов смещения поверхностной ионной плоскости относительно своего
объемного положения на величину
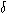 приводит к дополнительному вкладу
в величину дипольного барьера:
приводит к дополнительному вкладу
в величину дипольного барьера:
 |
(12) |
где d - межплоскостное расстояние.
В результате величина дипольного потенциального барьера определяется
суммой вкладов:
 Химический потенциал
Химический потенциал  электронного газа определяется своим
объемным значением:
электронного газа определяется своим
объемным значением:

где w - плотность объемной энергии кристалла.
В приближении локальной плотности объемная энергия металла, приходящаяся на
один атом и
выраженная через параметр плотности rs
 ,
определяется выражением:
,
определяется выражением:
 |
(13) |
В результате выражение для химического потенциала
 c учетом обменно-корреляционных и псевдопотенциальных поправок принимает вид:
c учетом обменно-корреляционных и псевдопотенциальных поправок принимает вид:
 |
(14) |
В настоящей работе для определения параметров псевдопотенциала Хейне-Абаренкова использовалось условие минимума объемной энергии металла. Минимизация соотношения (13) по rs приводит к выражению, связывающему V0 и Rm. Второй параметр определялся из сопоставления расчетных и экспериментальных значений поверхностной энергии. Методика расчета поверхностной энергии и параметров псевдопотенциала Хейне-Абаренкова изложены в нашей работе [2]. С целью улучшения количественного согласия значений поверхностной энергии для переходных и благородных металлов нами в данной работе был проведен учет влияния на поверхностные характеристики члена четвертого порядка по степеням градиента n(z) в разложении функционала полной энергии [3]. Результаты расчета приведены в табл.1. Видно, что для простых металлов наилучшим является использование градиентных поправок только второго порядка. Для Al необходим учет градиентных поправок четвертого порядка к кинетической энергии, что обусловлено большей неоднородностью электронного газа при s-p гибридизации квантовых состояний электронов. Для благородных и переходных металлов наилучшее согласие с экспериментальными значениями поверхностной энергии было получено при использовании градиентных поправок четвертого порядка к кинетической и обменно-корреляционной энергиям, что обусловлено эффектами s-p-d гибридизации.
Необходимые для вычисления высоты потенциального барьера D значения
вариационных параметров  и
и 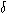 в данной работе определялись при
минимизации поверхностной энергии и приведены в табл.2.
Видно, что без учета эффектов смещения поверхностной
ионной плоскости получается хорошее согласие результатов расчета с
экспериментальными значениями работы выхода для
простых металлов и значительное их завышение для переходных.
Учет эффектов релаксации поверхности приводит к соответствию
значений для переходных металлов, но занижает их для простых.
В связи с сильной зависимостью величины работы выхода от
смещения ионной плоскости (от 20 до 50 %)
возникает необходимость
более точного, по сравнению с поверхностной энергией, определения
параметра релаксации. Для этого, по-видимому, необходимо учесть
эффекты смещения нескольких ионных приповерхностных слоев.
в данной работе определялись при
минимизации поверхностной энергии и приведены в табл.2.
Видно, что без учета эффектов смещения поверхностной
ионной плоскости получается хорошее согласие результатов расчета с
экспериментальными значениями работы выхода для
простых металлов и значительное их завышение для переходных.
Учет эффектов релаксации поверхности приводит к соответствию
значений для переходных металлов, но занижает их для простых.
В связи с сильной зависимостью величины работы выхода от
смещения ионной плоскости (от 20 до 50 %)
возникает необходимость
более точного, по сравнению с поверхностной энергией, определения
параметра релаксации. Для этого, по-видимому, необходимо учесть
эффекты смещения нескольких ионных приповерхностных слоев.
| [1] | Lang N.D., Kohn W. // Phys.Rev. 1971. B 3. P. 1215. |
| [2] | Мамонова M.В, Потерин Р.В, Прудников В.В. Расчет поверхностной энергии металлов в рамках модели обобщенного псевдопотенциала Хейне-Абаренкова. // Вестник Омского университета. 1996. N 1. C.41-43. |
| [3] | Вакилов А.Н., Прудников В.В., Прудникова М.В. Расчет решеточной релаксации металлических поверхностей с учетом влияния градиентных поправок на неоднородность электронной системы // ФММ. 1993. 76. N 6. C.38-48. |