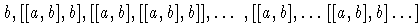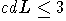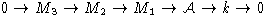Вестник Омского университета, 1998,
Вып. 1. С. 17-19.
© Омский государственный университет, 1998 |
УДК 519.49 |
Применение метода композиций в гомологической алгебре
М.А.Шевелин
Омский государственный университет, кафедра алгебры
644077, Омск, пр. Мира, 55-A
Получена 26 ноября 1997 г.
| The so called "method of compositions", developed by Shirhov, Bergman and
Bocut, since has had a numerous of applications in ring theory. In the
article we show that it is now proved to have one more. Namely, it allows in
some cases, to build free resolvents for modules over Lie or augmented
associative algebra. An example of such building is considered. |
1. Способ строить резольвенты
Пусть k - поле,
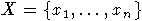 - конечный алфавит. Обозначим через F свободную ассоциативную алгебру
- конечный алфавит. Обозначим через F свободную ассоциативную алгебру
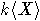 ,
, 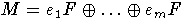 -свободный правый F-модуль, A=M+F
- соответствующее полупрямое произведение. Элементы A - это линейные
комбинации слов
-свободный правый F-модуль, A=M+F
- соответствующее полупрямое произведение. Элементы A - это линейные
комбинации слов
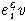 ,
где
,
где 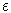 - нуль или единица,
а v - слово в алфавите X. Положим
- нуль или единица,
а v - слово в алфавите X. Положим
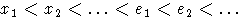 и продолжим этот порядок до полного порядка на словах так, чтобы слова
меньшей степени были меньше, а слова одинаковой степени были упорядочены
лексикографически слева направо. Старшее слово (без коэффициента) в смысле
этого порядка - действительно входящее в запись элемента
и продолжим этот порядок до полного порядка на словах так, чтобы слова
меньшей степени были меньше, а слова одинаковой степени были упорядочены
лексикографически слева направо. Старшее слово (без коэффициента) в смысле
этого порядка - действительно входящее в запись элемента
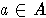 ,
называется старшим членом a и обозначается
,
называется старшим членом a и обозначается
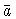 .
Элементы поля k будем обозначать строчными греческими буквами.
Пусть
.
Элементы поля k будем обозначать строчными греческими буквами.
Пусть 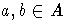 два элемента со старшими коэффициентами
два элемента со старшими коэффициентами 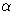 и
и 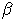 соответственно, причем
соответственно, причем 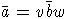 для некоторых, возможно, пустых слов v,w. Элемент
для некоторых, возможно, пустых слов v,w. Элемент
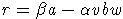 называется редукцией a относительно
b. Если
называется редукцией a относительно
b. Если 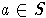 ,
то операцию
,
то операцию 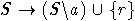 тоже будем называть редукцией.
тоже будем называть редукцией.
Пусть опять 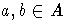 элементы со старшими коэффициентами
элементы со старшими коэффициентами 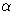 и
и 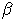 ,
,
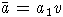 ,
,
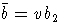 (a1,v,b2 - непустые слова).
Элемент
(a1,v,b2 - непустые слова).
Элемент 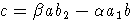 называется композицией a и b относительно v.
Обозначение: c=(a,b)v.
Символом
называется композицией a и b относительно v.
Обозначение: c=(a,b)v.
Символом
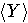 будем обозначать подмодуль, порожденный множеством Y, а
будем обозначать подмодуль, порожденный множеством Y, а
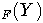 идеал в F, порожденный множеством Y.
идеал в F, порожденный множеством Y.
Определение 1. Множество 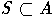 такое, что
такое, что 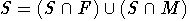 называется приведенным,
если между элементами S невозможны редукции. Приведенное множество S
называется замкнутым (относительно композиций), если для любой композиции
называется приведенным,
если между элементами S невозможны редукции. Приведенное множество S
называется замкнутым (относительно композиций), если для любой композиции
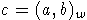 , элементов множества S,
приведенное множество, полученное из
, элементов множества S,
приведенное множество, полученное из 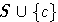 при помощи нескольких редукций, совпадает с
при помощи нескольких редукций, совпадает с 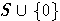 .
.
Лемма 1. Пусть 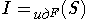 и
и 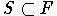 замкнуто условием
включения
замкнуто условием
включения 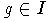 является
наличае в слове
является
наличае в слове 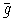 подслова вида
подслова вида 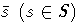 .
.
Следствие.
База алгебры 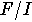 ,
в условиях леммы 1, состоит из всех слов в алфавите X,
не содержащих подслов вида
,
в условиях леммы 1, состоит из всех слов в алфавите X,
не содержащих подслов вида 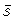
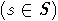 .
.
Лемма 2. Пусть  ,
,
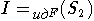 и множество
и множество
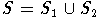 замкнуто.
Необходимым условием включнения
замкнуто.
Необходимым условием включнения 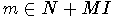 является наличае в слове
является наличае в слове 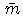 подслова вида
подслова вида 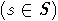 .
.
Лемма 1 и следствие хорошо известны [1], [5], а лемма 2
"покоординатная" переформулировка cледствия.
Рассмотрим алгебру F', поржденную множеством
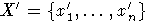 ,
гомоморфизм
,
гомоморфизм
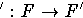
с ядром I, продолжающий биекцию
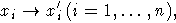
и свободный правый F'-модуль 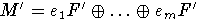 .
Пусть N' - подмодуль в M', порожденный множеством
.
Пусть N' - подмодуль в M', порожденный множеством
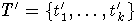 .
Предположим, что
.
Предположим, что
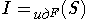 и множество
и множество 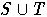 замкнуто. (T - подмножество в F, полученное из T' удалением
штрихов). Нас будет интересовать множество определяющих соотношений модуля
N'. Заметим, что из наших предположений следует, что S замкнуто.
Обозначим
замкнуто. (T - подмножество в F, полученное из T' удалением
штрихов). Нас будет интересовать множество определяющих соотношений модуля
N'. Заметим, что из наших предположений следует, что S замкнуто.
Обозначим 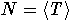 .
Определение 1 показывает, что для любой
композиции c=(ti,s)w,
.
Определение 1 показывает, что для любой
композиции c=(ti,s)w,
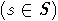 старший член
старший член 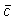 должен содержать подслово вида
должен содержать подслово вида 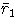
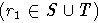 .
И после выполнения нескольких редукций:
.
И после выполнения нескольких редукций:
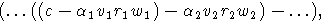
постоянно понижающих старший член, мы должны получить 0. Полученное таким
образом соотношение перепишем в виде:
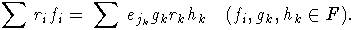
Множество левых частей этих соотношений обозначим буквой
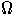 .
Очевидно,
.
Очевидно, 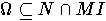 .
Заметим,что если
.
Заметим,что если
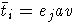 ,
,
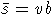 ,
то
,
то 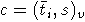 имеет меньший старший член, чем
имеет меньший старший член, чем
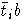 и поэтому все элементы множества
и поэтому все элементы множества
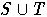 ,
относительно которых проводятся последующие редукции, имеют меньшие старшие члены,
чем
,
относительно которых проводятся последующие редукции, имеют меньшие старшие члены,
чем 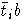 .
В частности, это касается элементов из T, относительно
которых проводятся редукции.
.
В частности, это касается элементов из T, относительно
которых проводятся редукции.
Лемма 3. 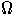 -
определяющее соотношение модуля
-
определяющее соотношение модуля 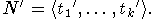
Доказательство. Нам нужно доказать, что
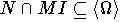 .
Возьмем элемент
.
Возьмем элемент 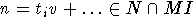 ,
где
,
где 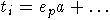 (a,v - слова в алфавите X, многоточиями обозначены младшие члены).
`По лемме 1
(a,v - слова в алфавите X, многоточиями обозначены младшие члены).
`По лемме 1 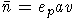 содержит подслово
содержит подслово 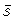 для некоторого
для некоторого 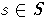 ,
а ссылаясь на следствие из леммы 1, мы можем предполагать, что
в словах a и v таких подслов нет. Поэтому возможна композиция
(ti,s) относительно подслова a2 слова a
(a=a1a2, a1 и
,
а ссылаясь на следствие из леммы 1, мы можем предполагать, что
в словах a и v таких подслов нет. Поэтому возможна композиция
(ti,s) относительно подслова a2 слова a
(a=a1a2, a1 и
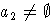 ).
В множестве
).
В множестве 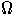 найдется элемент z, соответствующий этой композиции,
причем согласно замечанию, сделанному перед леммой 3, разность n-zv2
(v=a2v2, v2 может быть пустым) имеет меньший старший член, чем n,
а в остальном аналогична элементу n. За конечное число шагов мы выразим n
в виде правой линейной комбинации элементов
найдется элемент z, соответствующий этой композиции,
причем согласно замечанию, сделанному перед леммой 3, разность n-zv2
(v=a2v2, v2 может быть пустым) имеет меньший старший член, чем n,
а в остальном аналогична элементу n. За конечное число шагов мы выразим n
в виде правой линейной комбинации элементов
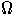 с коэффициентами в F.
Лемма доказана.
с коэффициентами в F.
Лемма доказана.
Из леммы 3 следует принадлежащая Левину [3] теорема о том, что
конечнопорожденные подмодули свободных F-модулей свободны.
2. Пример
Рассмотрим ассоциативную алгебру 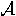 с 1 над полем характеристики 0 или больше 3, заданную порождающими и определяюшими
соотношениями:
с 1 над полем характеристики 0 или больше 3, заданную порождающими и определяюшими
соотношениями: 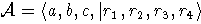 ,
где
,
где
r1=[[[a,b],b],b]+6[a,[a,b]];
r2=[b,[b,c]]-2b;
r3=[a,[b,c]]-4a;
r4=[a,c]-3b.
Здесь [x,y]=xy-yx.
Элементы алгебры 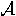 (точнее, их записи в виде многочленов от
(точнее, их записи в виде многочленов от 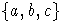 )
мы будем рассматривать иногда как элементы свободной ассоциативной алгебры
)
мы будем рассматривать иногда как элементы свободной ассоциативной алгебры
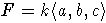 ,
это не должно вызвать недоразумений. Обозначим M1 свободный правый
,
это не должно вызвать недоразумений. Обозначим M1 свободный правый
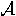 -модуль с базой
-модуль с базой 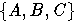 ,
,
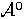 - ядро гомоморфизма k-алгебр
- ядро гомоморфизма k-алгебр 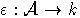 такого, что
такого, что 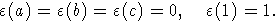
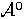 является правым идеалом в
является правым идеалом в 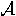 ,
порожденным
,
порожденным 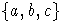 .
Гомоморфизм правых
.
Гомоморфизм правых 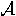 -модулей
-модулей 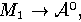 определенный правилом
определенный правилом
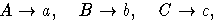
имеет ядро K1. Раскрывая коммутаторы в r1
- r4 и заменяя крайние левые буквы в словах на такие же
заглавные, мы получим элементы, порождающие модуль K1:
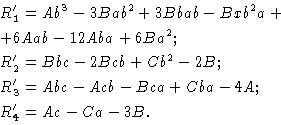
Обозначим M2 свободный 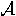 -модуль с базой
-модуль с базой 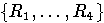 ,
а M3 - ядро гомоморфизма
,
а M3 - ядро гомоморфизма 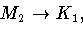 определенного условиями
определенного условиями

Лемма 4.
а) Множество 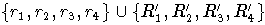 замкнуто (здесь
замкнуто (здесь 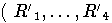 с
рассматриваются как элементы свободного правого F - модуля N
с базисом
с
рассматриваются как элементы свободного правого F - модуля N
с базисом 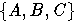 ).
б) Модуль M3 порожден элементами
).
б) Модуль M3 порожден элементами
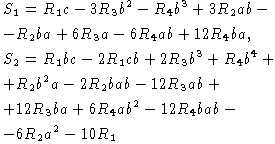
и является свободным с базисои 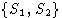 .
.
Доказательство. Непосредственно проверяется, что множество
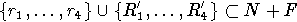
приведенное.
Возможны лишь четыре композиции между элементами этого множества:
(R'1,r2)b2,
(R'1,r2)b,
(r1,r2)b2,
(r1,r2)b.
Одна из возможных цепочек редукций для
(R'1,r2)b2:
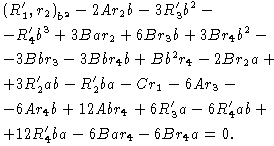
Цепочка редукций для (R'1,r2)b:
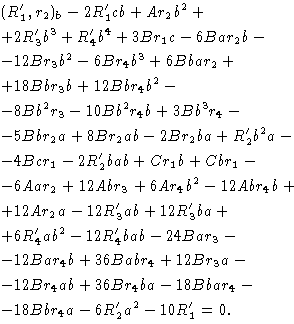
В случае остальных двух композиций вычисления отличаются только размерами
некоторых букв и отсутствием штрихов. Таким образом, а) доказано.
Чтобы доказать б), найдем определяющие соотношения подмодуля K1,
порожденного 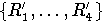 .
По лемме 4 достаточно в предыдущих двух длинных формулах все члены, содержащие одну из букв r,
заменить нулями. Это даст S1 и S2, если отбросить штрихи.
.
По лемме 4 достаточно в предыдущих двух длинных формулах все члены, содержащие одну из букв r,
заменить нулями. Это даст S1 и S2, если отбросить штрихи.
Наконец, множество 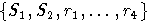 приведенное и замкнутое по причине отсутствия каких-нибудь композиций и редукций. Применяя снова
лемму 4, получаем, что между S1 и S2 никаких соотношений нет.
Поэтому M3 - свободный
приведенное и замкнутое по причине отсутствия каких-нибудь композиций и редукций. Применяя снова
лемму 4, получаем, что между S1 и S2 никаких соотношений нет.
Поэтому M3 - свободный 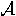 -модуль. Лемма доказана.
-модуль. Лемма доказана.
Пусть L будет алгебра Ли над полем K c порождающими a,b,c и
определяюшими соотношениями 1 - 4. Эта алгебра бесконечномерна, потому что
элементы
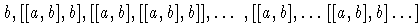 линейно независимы (это следует из [2]). Ее универсальная обертывающая
алгебра это
линейно независимы (это следует из [2]). Ее универсальная обертывающая
алгебра это 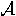 .
.
Согласно [4], проективной размерностью модуля называется наименьшая
длина его проективных резольвент.
Поле k можно наделить структурой L-модуля с помощью гомоморфизма
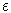 .
Тогда k становится
.
Тогда k становится 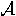 -модулем. Проективная размерность этого модуля называется когомологической размерностью
алгебры Ли L и обозначается cd L.
-модулем. Проективная размерность этого модуля называется когомологической размерностью
алгебры Ли L и обозначается cd L.
Теорема 1. 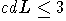
Доказательство. Точная последовательность
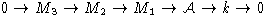
(все модули и стрелки определены перед леммой 4 или в ней самой) является
свободной резольвентой 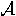 -модуля k.
-модуля k.
В заключение я благодарю Г.П. Кукина, под руководством которого была выполнена
эта работа.
Литература
| [1] |
Бокуть Л.А. Ассоциативные кольца. Новосибирск, 1977. |
| [2] |
Ширшов А.И. Некоторые алгоритмические проблемы для алгебр Ли // Сиб. Мат.
Журн. 1962. Т.3. N 2. |
| [3] |
Lewin J. Free modules over free algebras and free group algebras:
the Schreuer technique // Trans. Amer. Math. Soc. 145 (1969). P. 455-465. |
| [4] |
Картан, Эйленберг. Гомологическая алгебра. Москва: И. Л., 1960. |
| [5] |
Bocut L. Kukin G. Algorithmic and Combinatoral Algebra. Kluwer, 1994. |
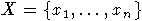 - конечный алфавит. Обозначим через F свободную ассоциативную алгебру
- конечный алфавит. Обозначим через F свободную ассоциативную алгебру
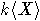 ,
, 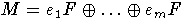 -свободный правый F-модуль, A=M+F
- соответствующее полупрямое произведение. Элементы A - это линейные
комбинации слов
-свободный правый F-модуль, A=M+F
- соответствующее полупрямое произведение. Элементы A - это линейные
комбинации слов
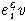 ,
где
,
где 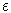 - нуль или единица,
а v - слово в алфавите X. Положим
- нуль или единица,
а v - слово в алфавите X. Положим
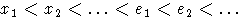 и продолжим этот порядок до полного порядка на словах так, чтобы слова
меньшей степени были меньше, а слова одинаковой степени были упорядочены
лексикографически слева направо. Старшее слово (без коэффициента) в смысле
этого порядка - действительно входящее в запись элемента
и продолжим этот порядок до полного порядка на словах так, чтобы слова
меньшей степени были меньше, а слова одинаковой степени были упорядочены
лексикографически слева направо. Старшее слово (без коэффициента) в смысле
этого порядка - действительно входящее в запись элемента
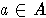 ,
называется старшим членом a и обозначается
,
называется старшим членом a и обозначается
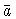 .
Элементы поля k будем обозначать строчными греческими буквами.
Пусть
.
Элементы поля k будем обозначать строчными греческими буквами.
Пусть 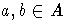 два элемента со старшими коэффициентами
два элемента со старшими коэффициентами 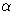 и
и 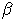 соответственно, причем
соответственно, причем 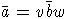 для некоторых, возможно, пустых слов v,w. Элемент
для некоторых, возможно, пустых слов v,w. Элемент
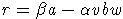 называется редукцией a относительно
b. Если
называется редукцией a относительно
b. Если 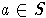 ,
то операцию
,
то операцию 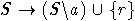 тоже будем называть редукцией.
тоже будем называть редукцией.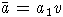 ,
,
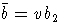 (a1,v,b2 - непустые слова).
Элемент
(a1,v,b2 - непустые слова).
Элемент 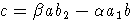 называется композицией a и b относительно v.
Обозначение: c=(a,b)v.
Символом
называется композицией a и b относительно v.
Обозначение: c=(a,b)v.
Символом
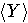 будем обозначать подмодуль, порожденный множеством Y, а
будем обозначать подмодуль, порожденный множеством Y, а
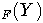 идеал в F, порожденный множеством Y.
идеал в F, порожденный множеством Y.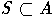 такое, что
такое, что 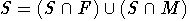 называется приведенным,
если между элементами S невозможны редукции. Приведенное множество S
называется замкнутым (относительно композиций), если для любой композиции
называется приведенным,
если между элементами S невозможны редукции. Приведенное множество S
называется замкнутым (относительно композиций), если для любой композиции
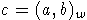 , элементов множества S,
приведенное множество, полученное из
, элементов множества S,
приведенное множество, полученное из 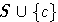 при помощи нескольких редукций, совпадает с
при помощи нескольких редукций, совпадает с 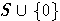 .
.
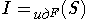 и
и 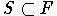 замкнуто условием
включения
замкнуто условием
включения 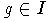 является
наличае в слове
является
наличае в слове 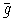 подслова вида
подслова вида 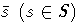 .
.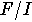 ,
в условиях леммы 1, состоит из всех слов в алфавите X,
не содержащих подслов вида
,
в условиях леммы 1, состоит из всех слов в алфавите X,
не содержащих подслов вида 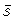
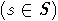 .
. ,
,
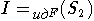 и множество
и множество
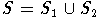 замкнуто.
Необходимым условием включнения
замкнуто.
Необходимым условием включнения 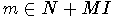 является наличае в слове
является наличае в слове 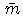 подслова вида
подслова вида 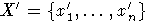 ,
гомоморфизм
,
гомоморфизм
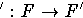
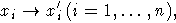
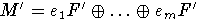 .
Пусть N' - подмодуль в M', порожденный множеством
.
Пусть N' - подмодуль в M', порожденный множеством
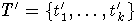 .
Предположим, что
.
Предположим, что
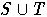 замкнуто. (T - подмножество в F, полученное из T' удалением
штрихов). Нас будет интересовать множество определяющих соотношений модуля
N'. Заметим, что из наших предположений следует, что S замкнуто.
Обозначим
замкнуто. (T - подмножество в F, полученное из T' удалением
штрихов). Нас будет интересовать множество определяющих соотношений модуля
N'. Заметим, что из наших предположений следует, что S замкнуто.
Обозначим 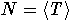 .
Определение 1 показывает, что для любой
композиции c=(ti,s)w,
.
Определение 1 показывает, что для любой
композиции c=(ti,s)w,
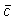 должен содержать подслово вида
должен содержать подслово вида 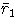
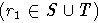 .
И после выполнения нескольких редукций:
.
И после выполнения нескольких редукций:
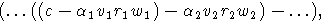
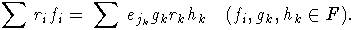
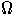 .
Очевидно,
.
Очевидно, 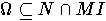 .
Заметим,что если
.
Заметим,что если
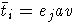 ,
,
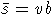 ,
то
,
то 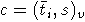 имеет меньший старший член, чем
имеет меньший старший член, чем
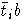 и поэтому все элементы множества
и поэтому все элементы множества
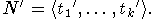
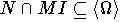 .
Возьмем элемент
.
Возьмем элемент 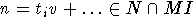 ,
где
,
где 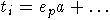 (a,v - слова в алфавите X, многоточиями обозначены младшие члены).
`По лемме 1
(a,v - слова в алфавите X, многоточиями обозначены младшие члены).
`По лемме 1 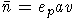 содержит подслово
содержит подслово 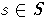 ,
а ссылаясь на следствие из леммы 1, мы можем предполагать, что
в словах a и v таких подслов нет. Поэтому возможна композиция
(ti,s) относительно подслова a2 слова a
(a=a1a2, a1 и
,
а ссылаясь на следствие из леммы 1, мы можем предполагать, что
в словах a и v таких подслов нет. Поэтому возможна композиция
(ti,s) относительно подслова a2 слова a
(a=a1a2, a1 и
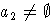 ).
В множестве
).
В множестве 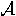 с 1 над полем характеристики 0 или больше 3, заданную порождающими и определяюшими
соотношениями:
с 1 над полем характеристики 0 или больше 3, заданную порождающими и определяюшими
соотношениями: 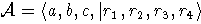 ,
где
,
где
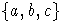 )
мы будем рассматривать иногда как элементы свободной ассоциативной алгебры
)
мы будем рассматривать иногда как элементы свободной ассоциативной алгебры
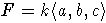 ,
это не должно вызвать недоразумений. Обозначим M1 свободный правый
,
это не должно вызвать недоразумений. Обозначим M1 свободный правый
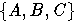 ,
,
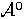 - ядро гомоморфизма k-алгебр
- ядро гомоморфизма k-алгебр 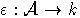 такого, что
такого, что 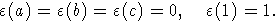
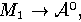 определенный правилом
определенный правилом
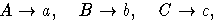
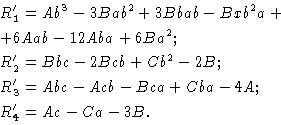
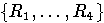 ,
а M3 - ядро гомоморфизма
,
а M3 - ядро гомоморфизма 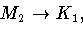 определенного условиями
определенного условиями

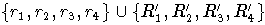 замкнуто (здесь
замкнуто (здесь 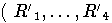 с
рассматриваются как элементы свободного правого F - модуля N
с базисом
с
рассматриваются как элементы свободного правого F - модуля N
с базисом 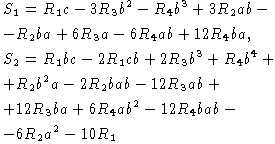
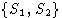 .
.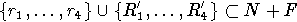
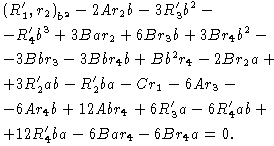
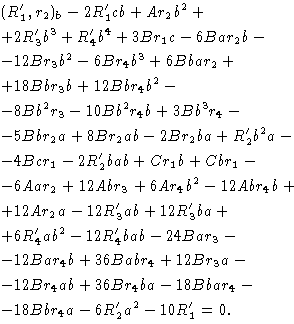
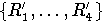 .
По лемме 4 достаточно в предыдущих двух длинных формулах все члены, содержащие одну из букв r,
заменить нулями. Это даст S1 и S2, если отбросить штрихи.
.
По лемме 4 достаточно в предыдущих двух длинных формулах все члены, содержащие одну из букв r,
заменить нулями. Это даст S1 и S2, если отбросить штрихи.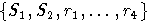 приведенное и замкнутое по причине отсутствия каких-нибудь композиций и редукций. Применяя снова
лемму 4, получаем, что между S1 и S2 никаких соотношений нет.
Поэтому M3 - свободный
приведенное и замкнутое по причине отсутствия каких-нибудь композиций и редукций. Применяя снова
лемму 4, получаем, что между S1 и S2 никаких соотношений нет.
Поэтому M3 - свободный