Вестник Омского
университета, 1998, Вып. 1. С. 14-16
© Омский государственный университет, 1998 |
УДК 519.48 |
Алгебраические автоморфизмы свободных алгебр
А.В.Фадин
Омский государственный университет, кафедра алгебры
644077, Омск, пр. Мира, 55-A
Получена 24 ноября 1997 г.
| We study in this paper a free algebras of finite rank,
their homomorphisms and endomorphisms |
1. Введение
Хорошо известна аналогия в строении свободных
алгебр следующих многообразий:
1) 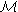 - многообразие всех алгебр над полем F;
- многообразие всех алгебр над полем F;
2)
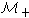 - многообразие всех коммутативных алгебр;
- многообразие всех коммутативных алгебр;
3)
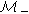 - многообразие всех антикоммутативных алгебр;
- многообразие всех антикоммутативных алгебр;
4) 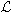 - многообразие всех алгебр Ли;
- многообразие всех алгебр Ли;
5) 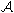 - многообразие алгебр с нулевым умножением.
- многообразие алгебр с нулевым умножением.
Для свободных алгебр
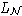 таких многообразий
таких многообразий 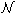 (где
(где 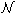 - одно из списка 1 - 5) справедлива
- одно из списка 1 - 5) справедлива
Теорема. (*) Любая подалгебра
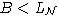 свободной алгебры является
свободной алгеброй того же многообразия.
свободной алгебры является
свободной алгеброй того же многообразия.
В случае 5 теория многообразия 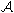 - это просто теория векторных
пространств (на которых определено нулевое умножение), и теорема(*) очевидна.
Для многообразия
- это просто теория векторных
пространств (на которых определено нулевое умножение), и теорема(*) очевидна.
Для многообразия 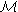 она доказана А.Г. Курошем. А для многообразий 2-4
А.И. Ширшовым. В 1993 г. У.У. Умирбаев нашел новые многообразия, где
выполнена Теорема(*).
она доказана А.Г. Курошем. А для многообразий 2-4
А.И. Ширшовым. В 1993 г. У.У. Умирбаев нашел новые многообразия, где
выполнена Теорема(*).
Гомоморфизмы алгебр в случае многообразия 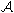 - это линейные отображения
(эндоморфизмы - любые линейные преобразования). Основная задача, которую мы
решаем в нашей работе,- обобщение теории линейных преобразований векторных
пространств (конечной размерности). В результате получается теория линейных
преобразований свободной алгебры
- это линейные отображения
(эндоморфизмы - любые линейные преобразования). Основная задача, которую мы
решаем в нашей работе,- обобщение теории линейных преобразований векторных
пространств (конечной размерности). В результате получается теория линейных
преобразований свободной алгебры
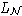 (где
(где 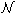 - многообразие из
списка 1 - 5). При этом аналогом размерности векторного пространства является
понятие ранга свободной алгебры
- многообразие из
списка 1 - 5). При этом аналогом размерности векторного пространства является
понятие ранга свободной алгебры
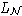 .
Ранг в данном случае - это
мощность множества свободных порождающих алгебры. В работе изучаются
свободные алгебры
.
Ранг в данном случае - это
мощность множества свободных порождающих алгебры. В работе изучаются
свободные алгебры
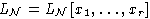 конечного ранга
r, их гомоморфизмы и эндоморфизмы.
конечного ранга
r, их гомоморфизмы и эндоморфизмы.
Чтобы избежать громоздких формулировок, мы все время говорим о свободных
алгебрах, в силу теоремы(*) все результаты справедливы для любого многообразия
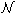 из списка 1-5 и для многообразий, открытых У.У. Умирбаевым.
из списка 1-5 и для многообразий, открытых У.У. Умирбаевым.
2. О 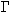 -цветных алгебрах
-цветных алгебрах
Определение 1. Пусть 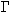 - группоид по умножению, F-произвольное поле.
Тогда алгебра A над полем F называется
- группоид по умножению, F-произвольное поле.
Тогда алгебра A над полем F называется
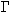 -цветной в том и только том случае, если
-цветной в том и только том случае, если
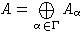 причем для любых
причем для любых
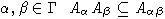
Определение 2. Пусть
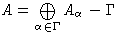 - цветная алгебра над полем
- цветная алгебра над полем 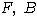 - ее подалгебра со свойством
- ее подалгебра со свойством
 .
Тогда подалгебра
B называется
.
Тогда подалгебра
B называется 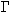 однородной (или однородной относительно раскраски).
однородной (или однородной относительно раскраски).
Определение 3. Пусть
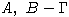 -цветные алгебры над одним и тем же полем
-цветные алгебры над одним и тем же полем
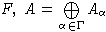
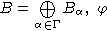 -линейное отображение из A в B. Если для любого
-линейное отображение из A в B. Если для любого
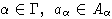 верно
верно
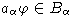 ,
то говорят, что отображение
,
то говорят, что отображение
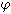 сохраняет раскраску.
сохраняет раскраску.
Определение 4. Пусть
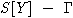 -цветная алгебра над полем F, порожденная множеством
-цветная алгебра над полем F, порожденная множеством
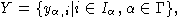
где
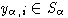 и зафиксировано вложение
и зафиксировано вложение
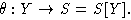 Если для любой
Если для любой 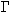 -цветной алгебры B над полем F любое отображение
-цветной алгебры B над полем F любое отображение
 (сохраняющее раскраску) продолжается до
гомоморфизма
(сохраняющее раскраску) продолжается до
гомоморфизма
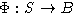 (сохраняющего раскраску), то алгебра S
называется свободной
(сохраняющего раскраску), то алгебра S
называется свободной 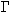 -цветной алгеброй со свободными
-цветной алгеброй со свободными 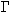 -цветными порождающими
-цветными порождающими
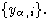
Пример 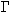 -цветной алгебры
-цветной алгебры
1. Пусть A=A[X] - свободная алгебра над полем F с множеством порождающих
X (или свободная ассоциативная алгебра, или свободная алгебра Ли, или
алгебра многочленов от X). Пусть N - группоид натуральных чисел (по
сложению), изоморфный мультипликативному группоиду
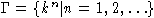 ,
где k - фиксированное комплексное число (
,
где k - фиксированное комплексное число (
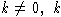 не является корнем из 1, т.е. группоид
не является корнем из 1, т.е. группоид 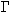 - бесконечный). Тогда
- бесконечный). Тогда
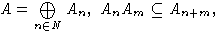 где An - векторное
пространство однородных элементов степени n. В этом случае A является
где An - векторное
пространство однородных элементов степени n. В этом случае A является
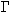 -цветной алгеброй:
-цветной алгеброй:
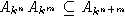 , где
, где
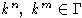 .
.
2. Пусть
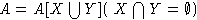 -свободная алгебра со свободными порождающими
-свободная алгебра со свободными порождающими
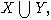
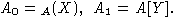 Тогда возьмем
Тогда возьмем
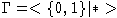 и получим
и получим 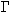 -цветную алгебру.
-цветную алгебру.
Определение 5. Пусть L - алгебра над полем
 -функция , которая имеет областью значений множество целых неотрицательных
чисел N* и обладает следующими свойствами:
-функция , которая имеет областью значений множество целых неотрицательных
чисел N* и обладает следующими свойствами:
1)
 не определено;
не определено;
2)
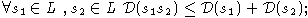
3)
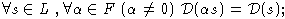
4)
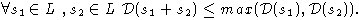
Тогда назовем 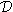 обобщенной степенью элемента s.
обобщенной степенью элемента s.
Примером, попадающим под определение обобщенной степени, может служить обычная
степень элемента.
Рассмотрим множество пар
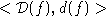 для всех элементов алгебры A, где
для всех элементов алгебры A, где
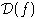 - обобщенная степень элемента
- обобщенная степень элемента
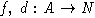 - обычная степень элемента алгебры. Это множество можно линейно упорядочить
таким образом:
- обычная степень элемента алгебры. Это множество можно линейно упорядочить
таким образом:

тогда и только тогда, когда 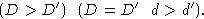
Пусть H - подалгебра свободной алгебры A. Построим счетную (или конечную)
последовательность таких пар 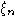 и последовательность подалгебр
и последовательность подалгебр
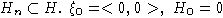 .
Если
.
Если 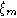 и Hm уже определены
для всех
и Hm уже определены
для всех 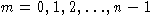 ,
то пусть
,
то пусть 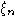 будет наименьшей парой,
соответствующей элементам из H, не вошедших в Hn-1, а Hn будет
подалгеброй, порожденной в H всеми элементами v, для которых
будет наименьшей парой,
соответствующей элементам из H, не вошедших в Hn-1, а Hn будет
подалгеброй, порожденной в H всеми элементами v, для которых
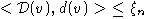 .
.
Лемма 1. Пусть A=A[X] - свободная алгебра над полем F
со свободными порождающими
 обобщенная степень на
алгебре A.
обобщенная степень на
алгебре A.
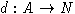 - функция, определяющая обычную степень элемента
алгебры A. Тогда произвольная подалгебра H<A обладает таким множеством
порождающих
- функция, определяющая обычную степень элемента
алгебры A. Тогда произвольная подалгебра H<A обладает таким множеством
порождающих
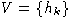 ,
что ни один элемент
,
что ни один элемент 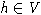 не принадлежит подалгебре, порожденной элементами
не принадлежит подалгебре, порожденной элементами
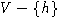 по модулю слагаемых той же
обобщенной степени, что и элемент h, но меньшей обычной степени или
меньшей обобщенной степени.
Следует заметить, что если алгебра
по модулю слагаемых той же
обобщенной степени, что и элемент h, но меньшей обычной степени или
меньшей обобщенной степени.
Следует заметить, что если алгебра
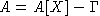 -цветная, а подалгебра
-цветная, а подалгебра
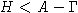 -однородная, то построенная конструкция дает множество
порождающих V подалгебры H, причем элементы
-однородная, то построенная конструкция дает множество
порождающих V подалгебры H, причем элементы
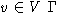 -однородны. То есть
-однородны. То есть
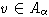 для некоторого
для некоторого
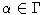 .
.
Лемма 2. Всякая подалгебра H свободной алгебры A свободна.
Доказательство этого факта можно найти в [1, 2].
Лемма 3. Пусть 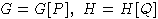 - свободные алгебры над одним и тем же полем F
с множеством свободных порождающих P и Q соответственно,
- свободные алгебры над одним и тем же полем F
с множеством свободных порождающих P и Q соответственно,
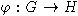 - гомоморфизм алгебр. Тогда
G=G1 * G0 (т.е. найдется такое множество
свободных порождающих R алгебры G, что
- гомоморфизм алгебр. Тогда
G=G1 * G0 (т.е. найдется такое множество
свободных порождающих R алгебры G, что
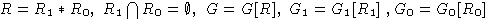 ,
причем
,
причем 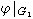 - изоморфизм G1 и
- изоморфизм G1 и 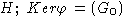 .
.
Теорема 1. (основная теорема о свободных цветных алгебрах).
Пусть L=L[X]- свободная алгебра над полем F с множеством свободных
порождающих X. Пусть, кроме того,
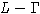 -цветная алгебра. Тогда L является свободной
-цветная алгебра. Тогда L является свободной
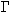 -цветной алгеброй.
-цветной алгеброй.
3. Основные результаты
Определение 6.
Пусть L - алгебра над полем
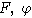 - ее эндоморфизм.
Тогда
- ее эндоморфизм.
Тогда 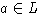 называется корневым элементом высоты n, если для некоторого
называется корневым элементом высоты n, если для некоторого
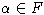 выполняется :
выполняется :
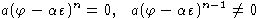
Определение 7.
Весом корневого элемента 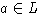 ,
отвечающего корню
,
отвечающего корню
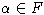 ,
назовем число w(a)=n-1, где n - высота элемента a.
,
назовем число w(a)=n-1, где n - высота элемента a.
Лемма 4.
Пусть L - свободная алгебра над полем F, 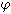 - ее эндоморфизм. Пусть
- ее эндоморфизм. Пусть 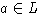 - элемент веса n-1, то есть
- элемент веса n-1, то есть
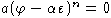
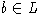 - элемент веса m-1, то есть
- элемент веса m-1, то есть
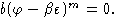
Тогда
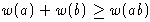 .
.
Лемма 5.
Пусть L - свободная алгебра конечного ранга над алгебраически
замкнутым полем F, 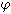 - ее алгебраический автоморфизм. Тогда
найдется собственный примитивный элемент алгебры L, то есть для некоторого
множества свободных порождающих
- ее алгебраический автоморфизм. Тогда
найдется собственный примитивный элемент алгебры L, то есть для некоторого
множества свободных порождающих
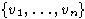 алгебры L
алгебры L
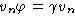 .
.
Лемма 6. (О триангуляции)
Пусть
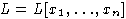 - свободная алгебра конечного ранга над алгебраически замкнутым полем
- свободная алгебра конечного ранга над алгебраически замкнутым полем
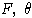 - ее алгебраический автоморфизм.
Тогда существует такое множество свободных порождающих
- ее алгебраический автоморфизм.
Тогда существует такое множество свободных порождающих
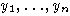 алгебры L, что
алгебры L, что
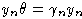 (для некоторого
(для некоторого
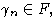 )
)
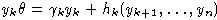 (для некоторых
(для некоторых
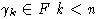 ).
).
Теорема 2.
Пусть
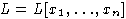 - свободная алгебра конечного ранга над алгебраически замкнутым полем
- свободная алгебра конечного ранга над алгебраически замкнутым полем
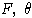 - ее алгебраический автоморфизм.
Причем для некоторого множества свободных порождающих
- ее алгебраический автоморфизм.
Причем для некоторого множества свободных порождающих
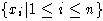
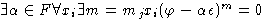 ,
где
,
где 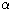 не является корнем из единицы. Тогда для некоторого множества
свободных порождающих
не является корнем из единицы. Тогда для некоторого множества
свободных порождающих
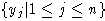 линейная оболочка
линейная оболочка
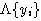 множества свободных порождающих инвариантна относительно
множества свободных порождающих инвариантна относительно
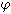 .
.
Из леммы 6 следует, что
.
.
Из леммы 6 следует, что
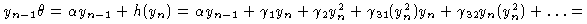
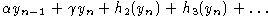 hi - однородная компонента степени i, относительно yn, поэтому
hi - однородная компонента степени i, относительно yn, поэтому
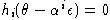 .
Получаем, что (если
.
Получаем, что (если
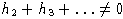 )
)
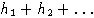 - собственный вектор
с собственным значением
- собственный вектор
с собственным значением 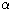 и в то же время сумма собственных векторов
относительно разных собсвенных чисел
и в то же время сумма собственных векторов
относительно разных собсвенных чисел
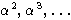 .
Противоречие, то есть
.
Противоречие, то есть
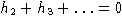 .
Это значит, что
.
Это значит, что
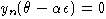 (собственный примитивный элемент)
(собственный примитивный элемент)
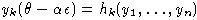 .
На самом деле верна следующая теорема.
.
На самом деле верна следующая теорема.
Теорема 3.
Пусть
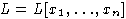 - свободная алгебра конечного ранга над
алгебраически замкнутым полем
- свободная алгебра конечного ранга над
алгебраически замкнутым полем
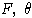 - ее алгебраический эндоморфизм.
Тогда L=L0*L1, где L0 - инвариантно относительно
- ее алгебраический эндоморфизм.
Тогда L=L0*L1, где L0 - инвариантно относительно
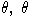 действует на L0 нильпотентно,
действует на L0 нильпотентно,
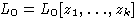 для некоторого
множества свободных порождающих
для некоторого
множества свободных порождающих
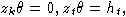 где
где
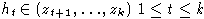 L1 имеет множество свободных порождающих, причем
L1 имеет множество свободных порождающих, причем
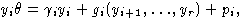 где
где
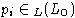 .
Из леммы 3 следует, что L распадается в свободное произведение L0 * L1,
где
.
Из леммы 3 следует, что L распадается в свободное произведение L0 * L1,
где
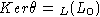 .
Тогда L0 инвариантна относительно
.
Тогда L0 инвариантна относительно
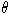 и действует на L0 нильпотентно. Профакторизуем L по L0, тогда можно
считать, что
и действует на L0 нильпотентно. Профакторизуем L по L0, тогда можно
считать, что 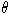 индуцирует на фактор-алгебре
индуцирует на фактор-алгебре
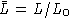 автоморфизм
автоморфизм
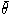 .
Применим лемму 6. Из нее следует, что для некоторого множества
свободных порождающих
.
Применим лемму 6. Из нее следует, что для некоторого множества
свободных порождающих
 алгебры
алгебры 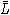 выполнено:
выполнено:
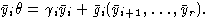
Сделав обратное отображение, получаем условие теоремы.
Литература
| [1] |
Ширшов А.И. Подалгебры свободных лиевых алгебр // Избр. тр. М.: Наука, 1984. |
| [2] |
Курош А.Г. Неассоциативные свободные алгебры и свободные произведения алгебр // Мат. сб. 1954. Т. 34(76).  1. С. 81-88. 1. С. 81-88. |
| [3] |
Михалев А.А. Подалгебры свободных цветных супералгебр Ли // Мат. заметки. 1985. Т. 37. 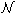 5. С. 653-659. 5. С. 653-659. |
| [4] |
Чирков И.В. О группах автоморфизмов свободных и свободных многоцветных алгебр. М., 1990. Деп. в ВИНИТИ 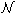 2098-B90. 2098-B90. |
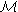 - многообразие всех алгебр над полем F;
- многообразие всех алгебр над полем F;
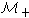 - многообразие всех коммутативных алгебр;
- многообразие всех коммутативных алгебр;
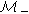 - многообразие всех антикоммутативных алгебр;
- многообразие всех антикоммутативных алгебр;
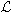 - многообразие всех алгебр Ли;
- многообразие всех алгебр Ли;
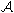 - многообразие алгебр с нулевым умножением.
- многообразие алгебр с нулевым умножением.
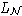 таких многообразий
таких многообразий 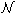 (где
(где 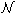 - одно из списка 1 - 5) справедлива
- одно из списка 1 - 5) справедлива
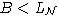 свободной алгебры является
свободной алгеброй того же многообразия.
свободной алгебры является
свободной алгеброй того же многообразия.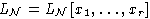 конечного ранга
r, их гомоморфизмы и эндоморфизмы.
конечного ранга
r, их гомоморфизмы и эндоморфизмы.
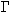 -цветных алгебрах
-цветных алгебрах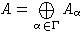 причем для любых
причем для любых
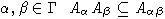
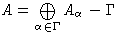 - цветная алгебра над полем
- цветная алгебра над полем 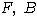 - ее подалгебра со свойством
- ее подалгебра со свойством
 .
Тогда подалгебра
B называется
.
Тогда подалгебра
B называется 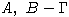 -цветные алгебры над одним и тем же полем
-цветные алгебры над одним и тем же полем
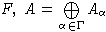
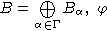 -линейное отображение из A в B. Если для любого
-линейное отображение из A в B. Если для любого
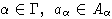 верно
верно
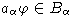 ,
то говорят, что отображение
,
то говорят, что отображение
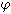 сохраняет раскраску.
сохраняет раскраску.
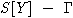 -цветная алгебра над полем F, порожденная множеством
-цветная алгебра над полем F, порожденная множеством
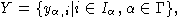
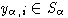 и зафиксировано вложение
и зафиксировано вложение
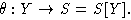 Если для любой
Если для любой  (сохраняющее раскраску) продолжается до
гомоморфизма
(сохраняющее раскраску) продолжается до
гомоморфизма
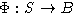 (сохраняющего раскраску), то алгебра S
называется свободной
(сохраняющего раскраску), то алгебра S
называется свободной 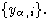
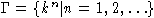 ,
где k - фиксированное комплексное число (
,
где k - фиксированное комплексное число (
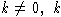 не является корнем из 1, т.е. группоид
не является корнем из 1, т.е. группоид 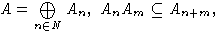 где An - векторное
пространство однородных элементов степени n. В этом случае A является
где An - векторное
пространство однородных элементов степени n. В этом случае A является
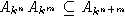 , где
, где
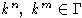 .
.
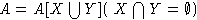 -свободная алгебра со свободными порождающими
-свободная алгебра со свободными порождающими
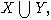
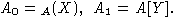 Тогда возьмем
Тогда возьмем
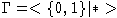 и получим
и получим  -функция , которая имеет областью значений множество целых неотрицательных
чисел N* и обладает следующими свойствами:
-функция , которая имеет областью значений множество целых неотрицательных
чисел N* и обладает следующими свойствами:
 не определено;
не определено;
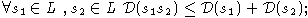
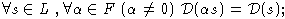
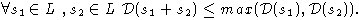
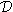 обобщенной степенью элемента s.
обобщенной степенью элемента s.
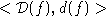 для всех элементов алгебры A, где
для всех элементов алгебры A, где
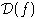 - обобщенная степень элемента
- обобщенная степень элемента
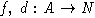 - обычная степень элемента алгебры. Это множество можно линейно упорядочить
таким образом:
- обычная степень элемента алгебры. Это множество можно линейно упорядочить
таким образом:

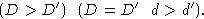
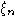 и последовательность подалгебр
и последовательность подалгебр
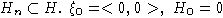 .
Если
.
Если 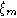 и Hm уже определены
для всех
и Hm уже определены
для всех 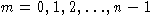 ,
то пусть
,
то пусть 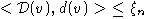 .
.
 обобщенная степень на
алгебре A.
обобщенная степень на
алгебре A. 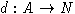 - функция, определяющая обычную степень элемента
алгебры A. Тогда произвольная подалгебра H<A обладает таким множеством
порождающих
- функция, определяющая обычную степень элемента
алгебры A. Тогда произвольная подалгебра H<A обладает таким множеством
порождающих
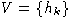 ,
что ни один элемент
,
что ни один элемент 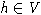 не принадлежит подалгебре, порожденной элементами
не принадлежит подалгебре, порожденной элементами
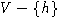 по модулю слагаемых той же
обобщенной степени, что и элемент h, но меньшей обычной степени или
меньшей обобщенной степени.
Следует заметить, что если алгебра
по модулю слагаемых той же
обобщенной степени, что и элемент h, но меньшей обычной степени или
меньшей обобщенной степени.
Следует заметить, что если алгебра
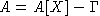 -цветная, а подалгебра
-цветная, а подалгебра
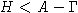 -однородная, то построенная конструкция дает множество
порождающих V подалгебры H, причем элементы
-однородная, то построенная конструкция дает множество
порождающих V подалгебры H, причем элементы
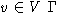 -однородны. То есть
-однородны. То есть
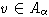 для некоторого
для некоторого
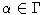 .
.
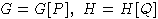 - свободные алгебры над одним и тем же полем F
с множеством свободных порождающих P и Q соответственно,
- свободные алгебры над одним и тем же полем F
с множеством свободных порождающих P и Q соответственно,
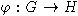 - гомоморфизм алгебр. Тогда
G=G1 * G0 (т.е. найдется такое множество
свободных порождающих R алгебры G, что
- гомоморфизм алгебр. Тогда
G=G1 * G0 (т.е. найдется такое множество
свободных порождающих R алгебры G, что
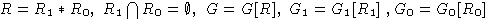 ,
причем
,
причем 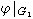 - изоморфизм G1 и
- изоморфизм G1 и 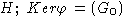 .
.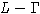 -цветная алгебра. Тогда L является свободной
-цветная алгебра. Тогда L является свободной
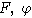 - ее эндоморфизм.
Тогда
- ее эндоморфизм.
Тогда 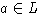 называется корневым элементом высоты n, если для некоторого
называется корневым элементом высоты n, если для некоторого
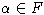 выполняется :
выполняется :
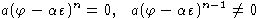
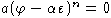
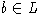 - элемент веса m-1, то есть
- элемент веса m-1, то есть
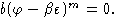
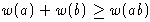 .
.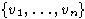 алгебры L
алгебры L
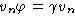 .
.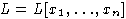 - свободная алгебра конечного ранга над алгебраически замкнутым полем
- свободная алгебра конечного ранга над алгебраически замкнутым полем
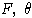 - ее алгебраический автоморфизм.
Тогда существует такое множество свободных порождающих
- ее алгебраический автоморфизм.
Тогда существует такое множество свободных порождающих
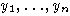 алгебры L, что
алгебры L, что
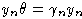
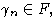 )
)
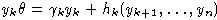
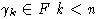 ).
).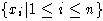
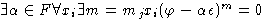 ,
где
,
где 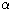 не является корнем из единицы. Тогда для некоторого множества
свободных порождающих
не является корнем из единицы. Тогда для некоторого множества
свободных порождающих
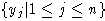 линейная оболочка
линейная оболочка
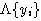 множества свободных порождающих инвариантна относительно
множества свободных порождающих инвариантна относительно
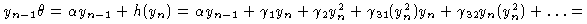
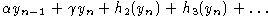 hi - однородная компонента степени i, относительно yn, поэтому
hi - однородная компонента степени i, относительно yn, поэтому
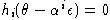 .
Получаем, что (если
.
Получаем, что (если
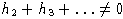 )
)
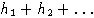 - собственный вектор
с собственным значением
- собственный вектор
с собственным значением 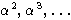 .
Противоречие, то есть
.
Противоречие, то есть
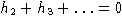 .
Это значит, что
.
Это значит, что
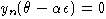 (собственный примитивный элемент)
(собственный примитивный элемент)
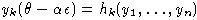 .
На самом деле верна следующая теорема.
.
На самом деле верна следующая теорема.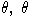 действует на L0 нильпотентно,
действует на L0 нильпотентно,
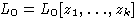 для некоторого
множества свободных порождающих
для некоторого
множества свободных порождающих
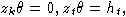 где
где
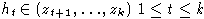 L1 имеет множество свободных порождающих, причем
L1 имеет множество свободных порождающих, причем
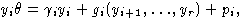 где
где
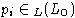 .
Из леммы 3 следует, что L распадается в свободное произведение L0 * L1,
где
.
Из леммы 3 следует, что L распадается в свободное произведение L0 * L1,
где
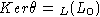 .
Тогда L0 инвариантна относительно
.
Тогда L0 инвариантна относительно
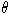 и действует на L0 нильпотентно. Профакторизуем L по L0, тогда можно
считать, что
и действует на L0 нильпотентно. Профакторизуем L по L0, тогда можно
считать, что 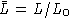 автоморфизм
автоморфизм
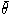 .
Применим лемму 6. Из нее следует, что для некоторого множества
свободных порождающих
.
Применим лемму 6. Из нее следует, что для некоторого множества
свободных порождающих
 алгебры
алгебры 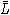 выполнено:
выполнено: